

分析 (1)先根据三角形内角和定理求得∠ABC+∠ACB,再根据角平分线的定义求得∠OBC+∠OCB,即可求出∠BOC.
(2)先根据三角形内角和定理求得∠ABC+∠ACB,再根据三等分线的定义求得∠O2BC+∠O2CB,即可求出∠BO2C.
(3)先根据三角形内角和定理求得∠ABC+∠ACB,再根据n等分线的定义求得∠On-1BC+∠On-1CB,即可求出∠BOn-1C.
(4)依据(3)的结论即可求出n的值.
解答 解:∵∠BAC=30°,
∴∠ABC+∠ACB=150°,
(1)∵点O是∠ABC与∠ACB的角平分线的交点,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=75°,
∴∠BOC=105°;
(2)∵点O2是∠ABC与∠ACB的三等分线的交点,
∴∠O2BC+∠O2CB=$\frac{2}{3}$(∠ABC+∠ACB)=100°,
∴∠BO2C=80°;
(3)∵点On-1是∠ABC与∠ACB的n等分线的交点,
∴∠On-1BC+∠On-1CB=$\frac{n-1}{n}$(∠ABC+∠ACB)=$\frac{n-1}{n}$×150°,
∴∠BOn-1C=180°-$\frac{n-1}{n}$×150°
(4)由(3)得:180°-$\frac{n-1}{n}$×150°=60°,
解得:n=5.
点评 本题主要考查等分线的性质以及三角形内角和定理,根据题意找出规律是解题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.
我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
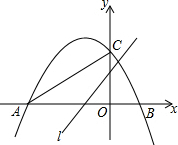 如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=$\sqrt{3}$x+m从点C开始沿y轴向下平移.
如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=$\sqrt{3}$x+m从点C开始沿y轴向下平移.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
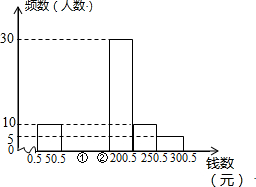 某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.| 分 组 | 频数 | 所占比例 |
| 0.5~50.5 | 10 | 0.1 |
| 50.5~100.5 | 20 | 0.2 |
| 100.5~150.5 | 35 | 35 |
| 150.5~200.5 | 30 | 0.3 |
| 200.5~250.5 | 10 | 0.1 |
| 250.5~300.5 | 5 | 0.05 |
| 合 计 | 100 | ------ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com