
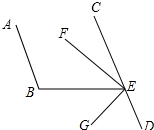
 如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.
如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数. 分析 首先根据平行线的性质可得∠B+∠CEB=180°,进而可得∠CEB的度数,再根据角平分线的定义可得∠FEB的度数,然后再根据垂直定义可得∠GEB的度数;利用邻补角的性质可得∠BED,再根据角的和差关系可得∠DEG的度数.
解答 解:∵AB∥CD,
∴∠B+∠CEB=180°,
∵∠B=96°,
∴∠CEB=180°-96°=84°,
∵EF平分∠BEC,
∴∠BEF=84°÷2=42°,
∵EG⊥EF,
∴∠FEG=90°,
∴∠BEG=90°-42°=48°,
∵∠CEB=84°,
∴∠BED=96°,
∴∠DEG=96°-48°=48°.
点评 此题主要考查了平行线的性质,以及角平分线定义,垂直定义,关键是掌握两直线平行,同旁内角互补.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④ | C. | ①③⑤ | D. | ①②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上,当∠A=30°,AC=10时,两直角顶点C,C1的距离是5.
如图所示是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上,当∠A=30°,AC=10时,两直角顶点C,C1的距离是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,AB=6,AD=8,∠ADC的平分线交BC于点F,交AB的延长线于点G,过点C作CE⊥DG,垂足为E,CE=2,则△BFG的周长为4+$\frac{8\sqrt{2}}{3}$.
如图,在?ABCD中,AB=6,AD=8,∠ADC的平分线交BC于点F,交AB的延长线于点G,过点C作CE⊥DG,垂足为E,CE=2,则△BFG的周长为4+$\frac{8\sqrt{2}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com