练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．下列图形：①等腰三角形；②平行四边形；③矩形；④菱形；⑤正方形．用两个全等但不是等腰的直角三角形，一定能拼成的是（　　）
    A．①②③B．②③④C．①③⑤D．①②③④⑤

    分析 根据等腰三角形、平行四边形、矩形、菱形、正方形的判定方法进行逐一分析即可．

    解答 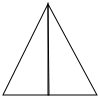解：①根据有两条边相等的三角形即为等腰三角形，所以能拼成等腰三角形，如图所示：②根据两组对边分别相等的四边形是平行四边形，则可以拼成平行四边形，如图所示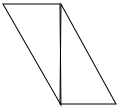：③根据有一个角是直角的平行四边形是矩形，则可以拼成矩形，如图所示：
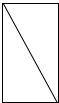    ④根据四条边相等的四边形才是菱形，而全等直角三角形的两条直角边不相等，所以不能拼成；
    ⑤根据有一个角是直角的菱形才是正方形，则不能拼成菱形，当然不能拼成正方形．
    故选：A．

    点评 本题考查了图形的剪拼，同时考查了学生的动手操作能力和想象观察能力，掌握等腰三角形、平行四边形、矩形、菱形、正方形的判定方法是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．在一次同学聚会上，若每两人握一次手，一共握了45次手，则参加这次聚会的同学一共有10名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，二次函数y=ax2+bx+c（a≠0）的大致图象，关于该二次函数下列说法正确的是（　　）
    A．a＞0，b＜0，c＞0B．当-1＜x＜2时，y＞0
    C．b2-4ac＜0D．当x＜$\frac{1}{2}$时，y随x的增大而减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．（1）计算：$\sqrt{9}$+（-$\frac{1}{2}$）-1-$\sqrt{2}$sin45°+（$\sqrt{3}$-2）0　　　　　　
    （2）解方程：$\frac{3}{x-1}=\frac{2}{x+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．对某班组织的一次考试成绩进行统计，已知80.5～90.5分这一组的频数是7，频率是0.2，那么该班级的人数是35人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，线段AB两个端点的坐标分别为A（4，4），B（6，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点C的坐标为（2，2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

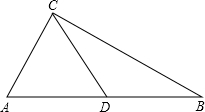    18．我们新定义一种三角形：两边平方和等于第三边平方的4倍的三角形叫做常态三角形．例如：某三角形三边长分别是5，6和8，因为62+82=4×52=100，所以这个三角形是常态三角形．
    （1）若△ABC三边长分别是2，$\sqrt{5}$和4，则此三角形是常态三角形（填“是”或“不是”）；
    （2）若Rt△ABC是常态三角形，则此三角形的三边长之比为$\sqrt{2}$：$\sqrt{3}$：$\sqrt{5}$（请按从小到大排列）；
    （3）如图，Rt△ABC中，∠ACB=90°，BC=6，点D为AB的中点，连接CD，若△BCD是常态三角形，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

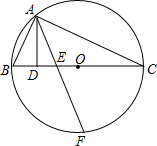    15．如图，△ABC内接于⊙O，且BC是⊙O的直径，AD⊥BC于D，F是弧BC中点，且AF交BC于E，连接OA，
    （1）求证：AE平分∠DAO；
    （2）若AB=6，AC=8，求OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，已知AB∥CD，∠B=96°，EF平分∠BEC，EG⊥EF，求∠BEG和∠DEG的度数．

    查看答案和解析>>

    同步练习册答案