
【题目】如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么? 
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少? 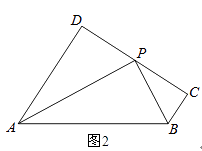
【答案】
(1)解:点P是线段CD的中点.理由如下:
过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC,
∵∠DAB的平分线与∠CBA的平分线交于点P,
∴PD=PE,PC=PE,
∴PC=PD,
∴点P是线段CD的中点;
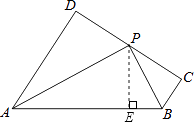
(2)解:过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC.
在△PBE与△PBC中,
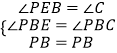 ,
,
∴△PBE≌△PBC(AAS),
∴∠EPB=∠CPB=35°,PE=PC,
∵PC=PD,
∴PD=PE,
在Rt△PAD与Rt△PAE中,
![]() ,
,
∴Rt△PAD≌Rt△PAE(HL),
∴∠APD=∠APE,
∵∠APD+∠APE=180°﹣2×35°=110°,
∴∠APD=55°,
∴∠PAD=90°﹣∠APD=35°.
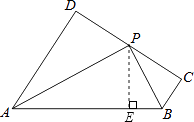
【解析】(1)过点P作PE⊥AB于E,根据平行线的性质求出∠C=90°,即PC⊥BC,再根据角平分线上的点到角的两边距离相等可得PD=PE,PC=PE,从而得到PC=PD,然后根据线段中点的定义解答;(2)过点P作PE⊥AB于E,根据平行线的性质求出∠C=90°,即PC⊥BC,利用AAS证明△PBE≌△PBC,得出∠EPB=∠CPB=35°,PE=PC,由PC=PD,等量代换得到PD=PE,再根据HL证明Rt△PAD≌Rt△PAE,得出∠APD=∠APE=55°,那么∠PAD=90°﹣∠APD=35°.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


科目:初中数学 来源: 题型:
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值.
(2)若用扇形统计图来描述,求分数在8≤m<9内所对应的扇形的圆心角的度数.
(3)将在第一组内的两名选手记为A1,A2,在第四组内的两名选手记为B1,B2, 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF. 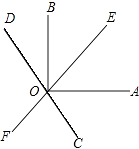
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数.(用含α的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com