
【题目】如图1,在平面直角坐标系中,点A,B,C的坐标分别是(0,a),(b,0),(a,﹣b)且a2+b2+4a﹣4b=﹣8,连接BC交y轴于点M,N为AC中点,连接NO并延长至D,使OD=ON,连接BD.
(1)求a,b的值;
(2)求∠DBC;
(3)如图2,Q为ON,BC的交点,连接AQ,AB,过点O作OP⊥OQ,交AB于P,过点O作OH⊥AB于H,交BQ于E,请探究线段EH,PH与OH之间有何数量关系?并证明你的结论.
【答案】解:(1)∵点A,B,C的坐标分别是(0,a),(b,0),(a,﹣b)且a2+b2+4a﹣4b=﹣8,
∴(a+2)2+(b﹣2)2=0,
∴a+2=0,b﹣2=0,
∴a=﹣2,b=2;
(2)∵A(0,﹣2),B(2,0),C(﹣2,﹣2),
∴AC∥x轴,
∵N为AC中点,
∴N(﹣1,﹣2),
∴AN=1,
∵OD=ON,
∴D和N点关于O点对称,
∴D(1,2),
设直线BD的解析式为y=k1x+b1 ,
∴![]() ,解得k1=﹣2,
,解得k1=﹣2,
设直线BC的解析式为y=k2x+b2 ,
∴![]() ,解得
,解得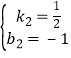 ,
,
∵k1k2=﹣1,
∴DB⊥BC,
∴∠DBC=90°;
(3)∵A(0,﹣2),B(2,0),
∴OA=OB=2,
∵OH⊥AB,
∴AH=BH,
∴H(1,﹣1),
∴直线OH:y=﹣x,OH=![]() ,
,
∵线BC的解析式为y=![]() x﹣1,
x﹣1,
解 得
得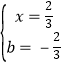 ,
,
∴E(![]() ,﹣
,﹣![]() ),
),
∴EH=![]() =
=![]() ,
,
∵N(﹣1,﹣2),
∴直线ON:y=2x,
∵OP⊥OQ,
∴直线OP:y=﹣![]() x,
x,
解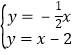 得
得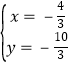 ,
,
∴P(![]() ,﹣
,﹣![]() ),
),
∴PH=![]() =
=![]() ,
,
∴OH﹣EH=2OH;
【解析】(1)把a2+b2+4a﹣4b=﹣8化成(a+2)2+(b﹣2)2=0,根据非负数的和等于0,即可求得a,b的值;
(2)根据A(0,﹣2),B(2,0),C(﹣2,﹣2),对称AC∥x轴,从而求得N的坐标,根据中心对称的性质对称D的坐标,然后根据待定系数法求得直线BD的斜率和直线BC的斜率,即可判定两条直线垂直,从而求得∠DBC=90°;
(3)分别求得E,H,P的坐标,根据勾股定理求得线段EH、OH、OH的长,即可得出线段EH,PH与OH之间的数量关系.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】
如图,以![]() 为直径的⊙O交△CFB的边
为直径的⊙O交△CFB的边![]() 于点A,
于点A, ![]() 平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC。
平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC。
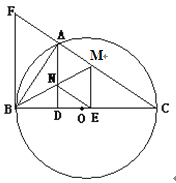
(1)证明:△ABM≌△EBM;
(2)证明:FB是⊙O的切线;
(3)若cos∠ABD=![]() ,AD=12.求四边形AMEN的面积S。
,AD=12.求四边形AMEN的面积S。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)已知函数![]() 求函数值的最大值;
求函数值的最大值;
(2)已知关于![]() 的函数
的函数![]() ,试求
,试求![]() 时函数值的最小值。
时函数值的最小值。
(3)已知直线![]() 和抛物线
和抛物线![]() 在
在![]() 轴左边交于
轴左边交于![]() 两点,直线
两点,直线![]() 过点
过点![]() 和线段
和线段![]() 的中点
的中点![]() ,求直线
,求直线![]() 与
与![]() 轴的交点纵坐标
轴的交点纵坐标![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.
(1)直接写出点A、B的坐标:A( ,),B( ,);
(2)请在图中确定点C(1,﹣2)的位置并连接AC、BC,则△ABC是三角形(判断其形状);
(3)在现在的网格中(包括网格的边界)存在一点P,点P的横纵坐标为整数,连接PA、PB后得到△PAB为等腰三角形,则满足条件的点P有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园歌手大奖赛上,比赛规则为:七位评委打分,去掉一个最高分和一个最低分后,所剩数据取平均数即为选手的最后得分.七位评委给某位歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0,则这位歌手的最后得分是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com