
如图,抛物线y=ax2+bx(a>0)经过原点O和点A(2,0).
(1)写出抛物线的对称轴与x轴的交点坐标;
(2)点(x1,y1),(x2,y2)在抛物线上,若x1<x2<1,比较y1,y2的大小;
(3)点B(﹣1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,求直线AC的函数关系式.
(1)(1,0);(2)y1>y2;(3)y=2x﹣4.
解析试题分析:(1)根据图示可以直接写出抛物线的对称轴与x轴的交点坐标;(2)根据抛物线的对称轴与x轴的交点坐标可以求得该抛物线的对称轴是x=1,然后根据函数图象的增减性进行解题;(3)根据已知条件可以求得点C的坐标是(3,2),所以根据点A、C的坐标来求直线AC的函数关系式.
试题解析:(1)根据图示,由抛物线的对称性可知,抛物线的对称轴与x轴的交点坐标(1,0).
(2)抛物线的对称轴是直线x=1.
根据图示知,当x<1时,y随x的增大而减小,∴当x1<x2<1时,y1>y2.
(3)∵对称轴是x=1,点B(﹣1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,
∴点C的坐标是(3,2).
设直线AC的关系式为y=kx+b(k≠0),则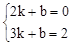 ,解得
,解得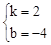 .
.
∴直线AC的函数关系式是:y=2x﹣4.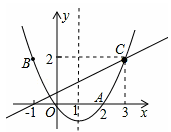
考点:1.抛物线与x轴的交点;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.二次函数的性质;5.轴对称的性质.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商店以16元/支的价格进了一批钢笔,如果以20元/支的价格售出,每月可以卖出200支,而每上涨1元就少卖10支,现在商店店主希望该笔月销售利润达1350元,则每支钢笔应该上涨多少元钱?请你就该种钢笔的涨价幅度和进货量,通过计算给店主提出一些合理建议.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看做一次函数:y=-10x+500.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(6分)
(2)如果李明想要每月获得2 000元的利润,那么销售单价应定为多少元?(3分)
(3)物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2 000元,那么他每月的成本最少需要多少元?(成本=进价×销售量) (3分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知关于 的一元二次方程
的一元二次方程 有实数根,
有实数根,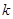 为正整数.
为正整数.
(1)求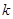 的值;
的值;
(2)当此方程有两个非零的整数根时,将关于 的二次函数
的二次函数 的图象向下平移8个单位,求平移后的图象的解析式;
的图象向下平移8个单位,求平移后的图象的解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某玩具批发商销售每件进价为40元的玩具,市场调查发现,若以每件50元的价格销售,平均每天销售90件,单价每提高1元,平均每天就少销售3件.
(1)平均每天的销售量y(件)与销售价x(元/件)之间的函数关系式为 ;
(2)求该批发商平均每天的销售利润W(元)与销售价x(元/件)之间的函数关系式;
(3)物价部门规定每件售价不得高于55元,当每件玩具的销售价为多少元时,可以获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲车在弯路做刹车试验,收集到的数据如下表所示:
速度 (千米/时) (千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | … |
刹车距离 (米) (米) | 0 |  | 2 |  | 6 |  | … |
 作为点的坐标,在如图所示的坐标系中画出刹车距离
作为点的坐标,在如图所示的坐标系中画出刹车距离 (米)与速度
(米)与速度 (千米/时)的函数图象,并求函数的解析式;
(千米/时)的函数图象,并求函数的解析式;
 (米)与速度
(米)与速度 (千米/时)满足函数
(千米/时)满足函数 ,请你就两车速度方面分析相撞原因.
,请你就两车速度方面分析相撞原因. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某文具店销售一种进价为10元/个的签字笔,物价部门规定这种签字笔的售价不得高于14元/个,根据以往经验:以12元/个的价格销售,平均每周销售签字笔100个;若每个签字笔的销售价格每提高1元,则平均每周少销售签字笔10个. 设销售价为x元/个.
(1)该文具店这种签字笔平均每周的销售量为 个(用含x的式子表示);
(2)求该文具店这种签字笔平均每周的销售利润w(元)与销售价x(元/个)之间的函数关系式;
(3)当x取何值时,该文具店这种签字笔平均每周的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com