
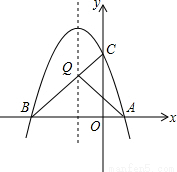
如图,抛物线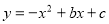 与x轴交与A(1,0),B(- 3,0)两点.
与x轴交与A(1,0),B(- 3,0)两点.
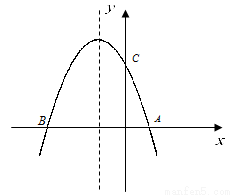
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.
(1)抛物线解析式为:y=-x2-2x+3;
(2)存在,Q(-1,2);
(3)存在,点P坐标为(-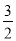 ,
,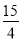 ),S△BPC最大=
),S△BPC最大=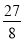 ;
;
【解析】
试题分析:(1)利用待定系数法求出抛物线解析式即可;
(2)由题知A、B两点关于抛物线的对称轴x=-1对称,直线BC与x=-1的交点即为Q点,此时△QAC的周长最小,首先求出直线BC的解析式,进而得出Q点坐标即可.
(3)存在,设得点P的坐标,将△BCP的面积表示成二次函数,根据二次函数最值的方法即可求得点P的坐标;
试题解析:(1)将A(1,0),B(-3,0)代y=-x2+bx+c中得
 ,
,
∴解得: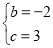 ,
,
∴抛物线解析式为:y=-x2-2x+3;
(2)存在,
由题知A、B两点关于抛物线的对称轴x=-1对称,
∴直线BC与x=-1的交点即为Q点,此时△AQC周长最小
∵y=-x2-2x+3,
∵C的坐标为:(0,3),B(-3,0),设直线BC解析式为:y=kx+d,
∴ ,
,
解得: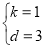 ,
,
∴直线BC解析式为:y=x+3;
Q点坐标即为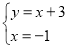 的解,
的解,
∴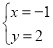 ,
,
∴Q(-1,2);
存在,如下图:
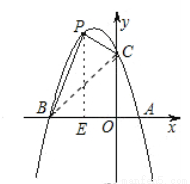
设P点(x,-x2-2x+3)(-3<x<0)
∵S△BPC=S四边形BPCO-S△BOC=S四边形BPCO-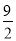 ,
,
若S四边形BPCO有最大值,则S△BPC就最大,
∴S四边形BPCO=S△BPE+S直角梯形PEOC=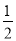 BEPE+
BEPE+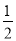 OE(PE+OC)=
OE(PE+OC)=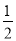 (x+3)(-x2-2x+3)+
(x+3)(-x2-2x+3)+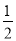 (-x)(-x2-2x+3+3)
(-x)(-x2-2x+3+3)
=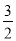 (x+
(x+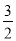 )2+
)2+ ,
,
当x=-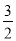 时,S四边形BPCO最大值=
时,S四边形BPCO最大值= ,
,
∴S△BPC最大= -
-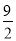 =
=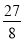 ,
,
当x=-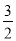 时,-x2-2x+3=
时,-x2-2x+3=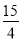 ,
,
∴点P坐标为(-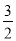 ,
,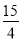 )
)
考点:1、待定系数法;2、线段的性质;3、二次函数的性质
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源:2014-2015学年河北省邯郸市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )
A.0.3× B.3×
B.3×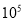 C.3×
C.3× D.30×
D.30×
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:填空题
用10米长的铝材制成一个矩形窗框,使它的面积为6平方米.若设它的一条边长为x 米,则根据题意可列出关于x的方程为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:选择题
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )

A.60° B.30° C.90° D.150°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
为解方程x4-5x2+4=0,我们可以将x2视为一个整体,然后设x2=y,则 x4=y2,
原方程化为y2-5y+4=0.①
解得y1=1,y2=4
当y=1时,x2=1.∴x=±1
当y=4时,x2=4,∴x=±2。
∴原方程的解为x1=1,x2=-1,x3=2,x4=-2
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用 法达到了降次的目的,体现了 的数学思想.
(2)解方程:(x2-2x)2+x2-2x-6=0.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(6分)国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.某中学为了了解学生体育活动情况,随机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”.以下是根据所得的数据制成的统计图的一部分.
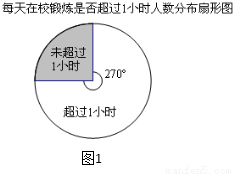
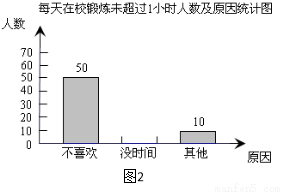
根据以上信息,解答下列问题:
(1)每天在校锻炼时间超过1小时的人数是 ;
(2)请将图2补充完整;
(3)2014年我市初中毕业生约为9.6万人,请你估计今年全市初中毕业生中每天锻炼时间超过1小时的学生约有多少万人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com