如图，直线l1// l2// l3，直线AC分别交l1， l2， l3于点A，B，C；直线DF分别交l1， l2， l3于点D，E，F .AC与DF相较于点H，且AH=2，HB=1，BC=5，则 
的值为（ ）
（A） （B）2
（C） （D）
科目：初中数学 来源： 题型：
如图，AB是⊙O的弦，AC是⊙Or切线，A为切点，BC经过圆心.若∠B=20°，则∠C的大小等于（ ）
A．20° B．25° C． 40° D．50°
查看答案和解析>>
科目：初中数学 来源： 题型：
已知关于x的一元二次方程
有两个不相等的实数根,k为正整数.
(1) 求k的值;
(2) 当此方程有一根为零时,直线y=x+2与关于x的二次函数y=
的图象交于A、B两点，若M是线段AB上的一个动点，过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值及此时点M的坐标;
(3) 将(2)中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分保持不变,翻折后的图象与原图象x轴上方的部分组成一个“W”形状的新图象，若直线y=
x+b与该新图象恰好有三个公共点，求b的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点
（1）已知点M，N是线段AB的勾股分割点，若AM=2，MN=3求BN的长；
（2）如图2，在△ABC中，FG是中位线，点D，E是线段BC的勾股分割点，且EC>DE≥BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点
（3）已知点C是线段AB上的一定点，其位置如图3所示，请在BC上画一点D，使C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画出一种情形即可）
（4）如图4，已知点M，N是线段AB的勾股分割点，MN>AM≥BN，△AMC，△MND
和△NBM均是等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，试探究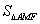
，
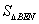和
的数量关系，并说明理由21教育网
查看答案和解析>>
科目：初中数学 来源： 题型：
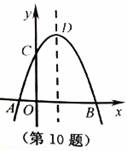
如图，抛物线y=-x2+2x+m+1交x轴于点A（a，0）和B（B，0），交y轴于点C，
抛物线的顶点为D.下列四个判断：①当x>0时，y>0；②若a=-1，则b=4；③抛物
线上有两点P（x1,y1）和Q（x2,y2），若x1<1< x2，且x1+ x2>2，则y1> y2；④点C关于
抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG
周长的最小值为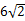
，其中正确判断的序号是（ ）
（A）① （B）②（C）③ （D）④
查看答案和解析>>
科目：初中数学 来源： 题型：
要估计鱼塘中的鱼数，养鱼者首先从鱼塘中打捞了50条鱼，在每条鱼身上做好记号后把这些鱼放归鱼塘，再从鱼塘中打捞100条，发现只有两条鱼是刚才做了记号的鱼，假设在鱼塘内鱼均匀分布，那么估计这个鱼塘的鱼数约为（ ）
A、5000条 B、2500条 C、1750条 D、1250条
查看答案和解析>>
科目：初中数学 来源： 题型：
如图 ，以线段AB为直径作⊙O ，CD与⊙O相切于点E ，交AB的延长线于点D , 连接BE ,过点O作
OC∥BE交切线DE于点C ,连接AC .
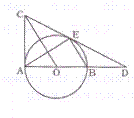(1)求证：AC是⊙O的切线 ； （2）若BD=OB=4 ,求弦AE的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
x2-1；