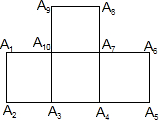
如图.在四个正方形拼接成的图形中.以这十个点中任意三点为顶点.共能组成( )个等腰直角三角形．A．18B．22C．24D．26 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

14．

如图，在四个正方形拼接成的图形中，以这十个点中任意三点为顶点，共能组成（　　）个等腰直角三角形．

A．

B．

C．

D．

分析分别找出以各角为直角顶点的等腰直角三角形的个数，再求出其和即可．

解答解：以A₁为直角顶点的等腰直角三角形有1个，以A₂为直角顶点的等腰直角三角形有1个，
以A₃为直角顶点的等腰直角三角形有2个，以A₄为直角顶点的等腰直角三角形有2个，
以A₅为直角顶点的等腰直角三角形有1个，以A₆为直角顶点的等腰直角三角形有1个，
以A₇为直角顶点的等腰直角三角形有6个，以A₈为直角顶点的等腰直角三角形有2个，
以A₉为直角顶点的等腰直角三角形有2个，以A₁₀为直角顶点的等腰直角三角形有6个，
故选C

点评此题主要考查学生对正文形的性质及等腰三角形的判定的综合运用，关键是找出以各角为直角顶点的等腰直角三角形的个数．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

9．

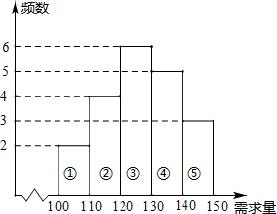经销商经销某种农产品，在一个销售月内，每售出1吨该产品获利500元，未售出的产品，每1吨亏损300元．根据历史资料记载的20个月的销售情况，得到如图所示的销售月内市场需求量的频数分布直方图．经销商为下一个销售月购进了130吨该农产品，以x（单位：吨，100≤x≤150）表示下一个销售月内的市场需求量，T（单位：元）表示下一个销售月内经销该农产品的利润．
完成下列问题：
（1）根据直方图可以看出，销售月内市场需求量的中位数在第③组．
（2）当100≤x≤150时，用含x的代数式或常数表示T；
（3）根据直方图估计利润T不少于57000元的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．如图，已知抛物线y=-x²+3x与x轴的正半轴交于点A，点B在抛物线上，且横坐标为2，作BC⊥x轴于点C，⊙B经过原点O，点E为⊙B上一动点，点F在AE上．
（1）求点A的坐标；
（2）如图1，连结OE，当AF：FE=1：2时，求证：△ACF∽△AOE；
（3）如图2，当点F是AE的中点时，求CF的最大值．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

2．在△ABC中，AB=BC=AC=6，则△ABC的面积为（　　）

A．

B．

C．

9$\sqrt{3}$

D．

18$\sqrt{3}$

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

9．下列计算正确的是（　　）

	A．	（x+y）（y-x）=x²-y²		B．	（x-2y）（x+2y）=x²-2y²
	C．	（2x-$\frac{1}{2}$y）²=4x²-2xy+$\frac{1}{4}$y²		D．	（-3x-2y）²=9x²-12xy+4y²

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，求BC的长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

如图，已知OA⊥OC，OB⊥OD，∠3=24°，求：∠1、∠2的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．利用网格点和三角板画图或计算：
（1）在给定方格纸中画出平移后的△A′B′C′；
（2）画出AB边上的中线CD；
（3）画出BC边上的高线AE；
（4）△A′B′C′的面积为8．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．计算：
（1）-1⁶-|-5|+2×（-$\frac{1}{2}$）²
（2）（$\frac{1}{3}$-$\frac{1}{4}$）÷（-$\frac{1}{12}$）+（-3）³÷（-3）
（3）2x-3（x-2y+3z）+2（3x-3y+2z）；
（4）$5{x^2}y-2xy-4（{{x^2}y-\frac{1}{2}xy}）$．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学