
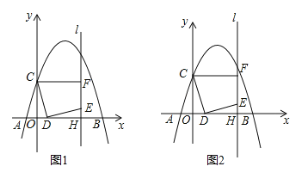
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������![]() ��x����A����1��0����B��5��0�����㣬��y���ڵ�C����D���߶�OB��һ���㣬����CD�����߶�CD�Ƶ�D˳ʱ����ת90��õ��߶�DE������E��ֱ��l��x����H������C��CF��l��F��
��x����A����1��0����B��5��0�����㣬��y���ڵ�C����D���߶�OB��һ���㣬����CD�����߶�CD�Ƶ�D˳ʱ����ת90��õ��߶�DE������E��ֱ��l��x����H������C��CF��l��F��
��1���������߽���ʽ��
��2����ͼ2������Fǡ������������ʱ�����߶�OD�ij���
��3���ڣ�2���������£�
������DF����tan��FDE��ֵ��
����̽����ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣿�����ڣ���ֱ��д����G�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��![]() ����2��1����3����
����2��1����3����![]() ����G��4��
����G��4��![]() ����4��6����
����4��6����
��������
�����������1����A��B��������������ߵĽ���ʽ���ⷽ�������ɣ�
��2����C�����������F�����꣬����OCD�ա�HDE���ó�DH=OC=3���������OD�ij���
��3������ȷ��C��D��E��F�ĵ㹲Բ����Բ�ܽǶ��������ECF=��EDF����tan��ECF=![]() =
=![]() ���õ�tan��FDE=
���õ�tan��FDE=![]() ��
��
������CE���ó���CDE�ǵ���ֱ�������Σ���CED=45�㣬��D����DG1��CE����ֱ��l��G1����D����DG2��CE����ֱ��l��G2������EDG1=45�㣬��EDG2=45�㣬���ֱ��CE�Ľ���ʽΪ![]() ����ֱ��DG1�Ľ���ʽΪ
����ֱ��DG1�Ľ���ʽΪ![]() ����ֱ��DG2�Ľ���ʽΪ
����ֱ��DG2�Ľ���ʽΪ![]() ����D��������뼴�����m��n���Ӷ���ý���ʽ���������G�����꣮
����D��������뼴�����m��n���Ӷ���ý���ʽ���������G�����꣮
�����������1����ͼ1����������![]() ��x����A����1��0����B��5��0�����㣬��
��x����A����1��0����B��5��0�����㣬��![]() �������
������� ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2����ͼ2������Fǡ�����������ϣ�C��0��3������F��������Ϊ3����y=3����![]() �ã�
�ã�![]() �����x=0��x=4����F��4��3������OH=4���ߡ�CDE=90�㣬���ODC+��EDH=90�㣬���OCD=��EDH������OCD����HDE�У��ߡ�OCD=��EDH����COD=��DHE=90����CD=DE�����OCD�ա�HDE��AAS������DH=OC=3����OD=4��3=1��
�����x=0��x=4����F��4��3������OH=4���ߡ�CDE=90�㣬���ODC+��EDH=90�㣬���OCD=��EDH������OCD����HDE�У��ߡ�OCD=��EDH����COD=��DHE=90����CD=DE�����OCD�ա�HDE��AAS������DH=OC=3����OD=4��3=1��
��3������ͼ3������CE���ߡ�OCD�ա�HDE����HE=OD=1����BF=OC=3����EF=3��1=2���ߡ�CDE=��CFE=90�㣬��C��D��E��F�ĵ㹲Բ�����ECF=��EDF����RT��CEF�У���CF=OH=4����tan��ECF=![]() =
=![]() ����tan��FDE=
����tan��FDE=![]() ��
��
����ͼ4������CE����CD=DE����CDE=90�㣬���CED=45�㣬��D����DG1��CE����ֱ��l��G1����D����DG2��CE����ֱ��l��G2������EDG1=45�㣬��EDG2=45������EH=1��OH=4����E��4��1������C��0��3������ֱ��CE�Ľ���ʽΪ![]() ����ֱ��DG1�Ľ���ʽΪ
����ֱ��DG1�Ľ���ʽΪ![]() ����D��1��0������
����D��1��0������![]() �����m=
�����m=![]() ����ֱ��DG1�Ľ���ʽΪ
����ֱ��DG1�Ľ���ʽΪ![]() ����x=4ʱ��
����x=4ʱ��![]() =
=![]() ����G1��4��
����G1��4��![]() ����
����
��ֱ��DG2�Ľ���ʽΪ![]() ����D��1��0������0=2��1+n�����n=��2����ֱ��DG2�Ľ���ʽΪ
����D��1��0������0=2��1+n�����n=��2����ֱ��DG2�Ľ���ʽΪ![]() ����x=4ʱ��y=2��4��2=6����G2��4��6����
����x=4ʱ��y=2��4��2=6����G2��4��6����
���ϣ���ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣬��G������Ϊ��4��![]() ����4��6����
����4��6����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ƽ��ÿ���ԭ�ƻ�������50̨��������������600̨��������Ҫ��ʱ����ԭ�ƻ�����450̨��������Ҫ��ʱ����ͬ��
��1��ԭ�ƻ�ƽ��ÿ����������̨������
��2�����ù���Ҫ�ڲ�����5���ʱ�䣬����1100̨��������ƽ��ÿ�����ٻ�Ҫ�ٶ���������̨������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�ǵȱ������Σ���D��E�ֱ��ڱ�AB��BC�ϣ�CD��AE���ڵ�F����AFD=60�㣮
��1����ͼ1����֤��BD=CE�� 
��2����ͼ2��FGΪ��AFC�Ľ�ƽ���ߣ���H��FG���ӳ����ϣ�HG=CD������HA��HC����֤����AHC=60�㣻 
��3���ڣ�2���������£���AD=2BD��FH=9����AF����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ��x�ᡢy��Ľ���ֱ�ΪA��B������OBA���ۣ�ʹ��O�Ķ�Ӧ��H����ֱ��AB�ϣ��ۺ۽�x���ڵ�C��
��x�ᡢy��Ľ���ֱ�ΪA��B������OBA���ۣ�ʹ��O�Ķ�Ӧ��H����ֱ��AB�ϣ��ۺ۽�x���ڵ�C��
��1��ֱ��д����C�����꣬�����A��B��C����������ߵĽ���ʽ��
��2���������ߵĶ���ΪD����ֱ��BC���Ƿ���ڵ�P��ʹ���ı���ODAPΪƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
��3���������ߵĶԳ�����ֱ��BC�Ľ���ΪT��QΪ�߶�BT��һ�㣬ֱ��д��|QA��QO|��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ����A��0��2����B��3��2�����㣬��������D��Eͬʱ��ԭ��O�ֱ�����x�ᡢy���������˶�����E���ٶ���ÿ��1����λ���ȣ���D���ٶ���ÿ��2����λ���ȣ�
����A��0��2����B��3��2�����㣬��������D��Eͬʱ��ԭ��O�ֱ�����x�ᡢy���������˶�����E���ٶ���ÿ��1����λ���ȣ���D���ٶ���ÿ��2����λ���ȣ�
��1������������x��Ľ������ꣻ
��2������CΪ��������x��Ľ��㣬�Ƿ���ڵ�D��ʹA��B��C��D�ĵ�Χ�ɵ��ı�����ƽ���ı��Σ������ڣ����D�����ꣻ�������ڣ�˵�����ɣ�
��3���ʼ�����ʱ��B��D��E��ͬһ��ֱ���ϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����ݣ�2��1��x��7��3��5��3��2��������2�����������ݵ���λ���ǣ� ��
A. 2 B. 2.5 C. 3 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������l1��y=ax2+bx+c��a��0������ԭ�㣬��x�����һ������ΪB��4��0������AΪ���㣬��ֱ��OA�Ľ���ʽΪy=x��

��1����ͼ1����������l1�Ľ���ʽ��
��2����ͼ2����������l1��ԭ��O��ת180�㣬�õ�������l2��l2��x�ύ�ڵ�B�䣬����ΪA�䣬��PΪ������l1��һ���㣬����PO��l2�ڵ�Q������PA��PA�䡢QA�䡢QA��
����ƽ���ı���PAQA������S��P�������x��2��x��4��֮��Ĺ�ϵʽ��
��3���ڣ�2���������£���ͼ11��3������BA�䣬������l1��l2���Ƿ����һ��H��ʹ��HB=HA�䣿�����ڣ��������H�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AC�Ĵ�ֱƽ���߷ֱ�AB��AC�ڵ�D��E�� 
��1������A=40�㣬���DCB�Ķ�����
��2����AE=4����DCB���ܳ�Ϊ13�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ŵ������( )
A. 3-4x=-(4x-3)
B. (a+b)-2a-b=(a+b)-(2a+b)
C. -x2+5x-4=-(x2-5x+4)
D. -a2+4a+a3-5=-(a2-4a)-(a3+5)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com