
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E. 
(1)若∠A=40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.
【答案】
(1)解:∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠ACB= ![]() =70°,
=70°,
∵DE垂直平分AC,
∴DA=DC,
∴在△DAC中,∠DCA=∠A=40°,
∴∠DCB=∠ACB﹣∠ACD=30°
(2)解:∵DE垂直平分AC,
∴DA=DC,EC=EA=4,
∴AC=2AE=8,
∴△ABC的周长为:AC+BC+BD+DA=8+BC+BD+DC=8+13=21
【解析】(1)由在△ABC中,AB=AC,∠A=40°,根据等腰三角形的性质,可求得∠ACB的度数,又由线段垂直平分线的性质,可得AD=CD,即可求得∠ACD的度数,继而求得答案;(2)由AE=4,△DCB的周长为13,即可求得△ABC的周长.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2008年春运期间,我国南方出现大范围冰雪灾害,导致某地电路断电.该地供电局组织电工进行抢修.供电局距离抢修工地15千米.抢修车装载着所需材料先从供电局出发,15分钟后,电工乘吉普车从同一地点出发,结果两车同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算及解方程:
(1)化简:(5a2﹣ab)﹣2(3a2﹣ ![]() ab)
ab)
(2)解方程: ![]() ﹣
﹣ ![]() =1
=1
(3)先化简,再求值:3x2y﹣[2xy﹣2(xy﹣ ![]() x2y)+xy],其中x=3,y=﹣
x2y)+xy],其中x=3,y=﹣ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
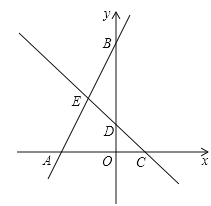
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程![]() 的两个根(OA>OC).
的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数![]() (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上书写了一个正确的演算过程,随后用一张纸挡住了一个二次三项式,形式如下: ![]() ﹣3x=x2﹣5x+1
﹣3x=x2﹣5x+1
(1)求所挡的二次三项式;
(2)若x=﹣1,求所挡的二次三项式的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com