
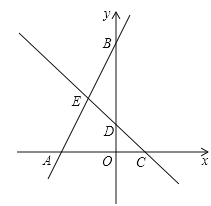
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程![]() 的两个根(OA>OC).
的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数![]() (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
【答案】(1)A(﹣2,0),C(1,0);(2)k=﹣2;(3)N的坐标为(![]() ,
, ![]() )、(
)、(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用分解因式法解一元二次方程![]() 即可得出OA、OC的值,再根据点所在的位置即可得出A、C的坐标;
即可得出OA、OC的值,再根据点所在的位置即可得出A、C的坐标;
(2)根据点C的坐标利用待定系数法即可求出直线CD的解析式,根据点A、B的横坐标结合点E为线段AB的中点即可得出点E的横坐标,将其代入直线CD的解析式中即可求出点E的坐标,再利用待定系数法即可求出k值;
(3)假设存在,设点M的坐标为(m,﹣m+1),分别以BE为边、BE为对角线来考虑.根据菱形的性质找出关于m的方程,解方程即可得出点M的坐标,再结合点B、E的坐标即可得出点N的坐标.
试题解析:(1)∵![]() ,∴(x﹣1)(x﹣2)=0,∴
,∴(x﹣1)(x﹣2)=0,∴![]() =1,
=1,![]() =2,∵OA>OC,∴OA=2,OC=1,∴A(﹣2,0),C(1,0).
=2,∵OA>OC,∴OA=2,OC=1,∴A(﹣2,0),C(1,0).
(2)将C(1,0)代入y=﹣x+b中,得:0=﹣1+b,解得:b=1,∴直线CD的解析式为y=﹣x+1.
∵点E为线段AB的中点,A(﹣2,0),B的横坐标为0,∴点E的横坐标为﹣1.
∵点E为直线CD上一点,∴E(﹣1,2).
将点E(﹣1,2)代入![]() (k≠0)中,得:2=
(k≠0)中,得:2=![]() ,解得:k=﹣2.
,解得:k=﹣2.
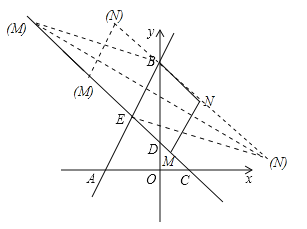
(3)假设存在,设点M的坐标为(m,﹣m+1),以点B,E,M,N为顶点的四边形是菱形分两种情况(如图所示):
①以线段BE为边时,∵E(﹣1,2),A(﹣2,0),E为线段AB的中点,∴B(0,4),∴BE=![]() AB=
AB=![]() =
=![]() .
.
∵四边形BEMN为菱形,∴EM=![]() =BE=
=BE=![]() ,解得:m1=
,解得:m1=![]() ,m2=
,m2=![]() ,∴M(
,∴M(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),∵B(0,4),E(﹣1,2),∴N(
),∵B(0,4),E(﹣1,2),∴N(![]() ,
, ![]() )或(
)或(![]() ,
,![]() );
);
②以线段BE为对角线时,MB=ME,∴![]() =
=![]() ,解得:m3=
,解得:m3=![]() ,∴M(
,∴M(![]() ,
,![]() ),∵B(0,4),E(﹣1,2),∴N(0﹣1+
),∵B(0,4),E(﹣1,2),∴N(0﹣1+![]() ,4+2﹣
,4+2﹣![]() ),即(
),即(![]() ,
,![]() ).
).
综上可得:坐标平面内存在点N,使以点B,E,M,N为顶点的四边形是菱形,点N的坐标为(![]() ,
, ![]() )、(
)、(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
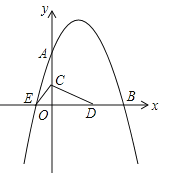
【题目】如图,已知抛物线![]() 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E. 
(1)若∠A=40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
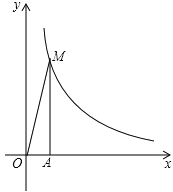
【题目】反比例函数![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数![]() 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.
(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数![]() 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形,属于因式分解的是( )
A. (a+1)(a-1)=a2-1 B. 2a-2b=2(a-b)
C. a2-2a+1=a(a-2)+1 D. a+2b=(a+b)+b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com