
【题目】△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.
(1)如图1,求证:BD=CE; 
(2)如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°; 
(3)在(2)的条件下,若AD=2BD,FH=9,求AF长.
【答案】
(1)解:如图1,
∵△ABC是等边三角形,
∴∠B=∠ACE=60°BC=AC,
∵∠AFD=∠CAE+∠ACD=60°∠BCD+∠ACD=∠ACB=60°,
∴∠BCD=∠CAE,
在△ABE和△BCD中,
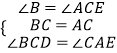
∴△ABE≌△BCD(ASA),
∴BD=CE;
(2)解:如图2,作CM⊥AE交AE的延长线于M,作CN⊥HF于N,

∵∠EFC=∠AFD=60°
∴∠AFC=120°,
∵FG为△AFC的角平分线,
∴∠CFH=∠AFH=60°,
∴∠CFH=∠CFE=60°,
∵CM⊥AE,CN⊥HF,
∴CM=CN,
∵∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,
∴∠CEM=∠CGN,
在△ECM和△GCN中
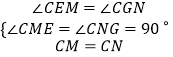
∴△ECM≌△GCN(AAS),
∴CE=CG,EM=GN,∠ECM=∠GCN,
∴∠MCN=∠ECG=60°,
∵△ABE≌△BCD,
∵AE=CD,
∵HG=CD,
∴AE=HG,
∴AE+EM=HG+GN,即AM=HN,
在△AMC和△HNC中
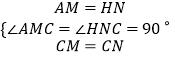
∴△AMC≌△HNC(SAS),
∴∠ACM=∠HCN,AC=HC,
∴∠ACM﹣∠ECM=∠HCN﹣∠GCN,即∠ACE=∠HCG=60°,
∴△ACH是等边三角形,
∴∠AHC=60°;
(3)解:如图3,在FH上截取FK=FC,
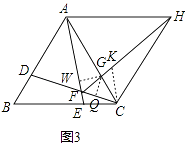
∵∠HFC=60°,
∴△FCK是等边三角形,
∴∠FKC=60°,FC=KC=FK,
∵∠ACH=60°,
∴∠ACF=∠HCK,
在△AFC和△HKC中
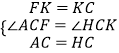
∴△AFC≌△HKC(SAS),
∴AF=HK,
∴HF=AF+FC=9,
∵AD=2BD,BD=CE=CG,AB=AC,
∴AG=2CG,
∴ ![]() =
= ![]() =
= ![]() ,
,
作GW⊥AE于W,GQ⊥DC于Q,
∵FG为△AFC的角平分线,
∴GW=GQ,
∵ ![]() =
= 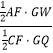 =
= ![]() =
= ![]() ,
,
∴AF=2CF,
∴AF=6.
【解析】(1)根据等边三角形的性质得出AB=BC,∠BAC=∠C=∠ABE=60°,根据SAS推出△ABE≌△BCD,即可证得结论;(2)根据角平分线的性质定理证得CM=CN,利用∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,得出∠CEM=∠CGN,然后根据AAS证得△ECM≌△GCN,得出CG=CE,EM=GN,∠ECM=∠GCN,进而证得△AMC≌△HNC,得出∠ACM=∠HCN,AC=HC,从而证得△ACH是等边三角形,证得∠AHC=60°;(3)在FH上截取FK=FC,得出△FCK是等边三角形,进一步得出FC=KC=FK,∠ACF=∠HCK,证得△AFC≌△HKC得出AF=HK,从而得到HF=AF+FC=9,由AD=2BD可知AG=2CG,再由 ![]() =
= ![]() ,根据等高三角形面积比等于底的比得出
,根据等高三角形面积比等于底的比得出 ![]() =
= 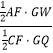 =
= ![]() =2,再由AF+FC=9求得.
=2,再由AF+FC=9求得.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
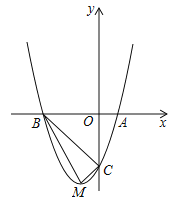
【题目】如图,顶点为M的抛物线![]() 分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)2(m+1)2﹣(2m+1)(2m﹣1);
(2)4x2﹣(﹣2x+3)(﹣2x﹣3);
(3)先化简,再求值:[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣2,y= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知抛物线![]() 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,![]() =5:6?
=5:6?
(3)图2所示的抛物线是由![]() 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上书写了一个正确的演算过程,随后用一张纸挡住了一个二次三项式,形式如下: ![]() ﹣3x=x2﹣5x+1
﹣3x=x2﹣5x+1
(1)求所挡的二次三项式;
(2)若x=﹣1,求所挡的二次三项式的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com