
【题目】如图1所示,已知抛物线![]() 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,![]() =5:6?
=5:6?
(3)图2所示的抛物线是由![]() 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.

【答案】(1)D(2,9),E(2,3);(2)![]() ,
,![]() ;(3)(1,1)或(3,3)或(2,2).
;(3)(1,1)或(3,3)或(2,2).
【解析】
试题分析:(1)把抛物线配方,即可得到顶点为D的坐标,然后设点E的坐标是(2,m),点C′的坐标是(0,n),根据△CEC′是等腰直角三角形,求出E点的坐标;
(2)令抛物线的y=0,可求得A、B的坐标,然后再根据![]() =5:6,得到:
=5:6,得到:![]() ,然后再证明△HGM∽△ABN,
,然后再证明△HGM∽△ABN,![]() ,从而可证得
,从而可证得![]() ,所以HG=5,设点H(m,﹣m2+4m+5),G(m,m+1),最后根据HG=5,列出关于m的方程求解即可;
,所以HG=5,设点H(m,﹣m2+4m+5),G(m,m+1),最后根据HG=5,列出关于m的方程求解即可;
(3)分别根据∠P、∠Q、∠T为直角画出图形,然后利用等腰直角三角形的性质和一次函数的图象的性质求得点Q的坐标即可.
试题解析:(1)∵抛物线![]() =
=![]() ,∴D点的坐标是(2,9),∵E为对称轴上的一点,∴点E的横坐标是2,设点E的坐标是(2,m),点C′的坐标是(0,n),∵将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上,∴△CEC′是等腰直角三角形,∴
,∴D点的坐标是(2,9),∵E为对称轴上的一点,∴点E的横坐标是2,设点E的坐标是(2,m),点C′的坐标是(0,n),∵将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上,∴△CEC′是等腰直角三角形,∴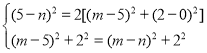 ,解得:
,解得:![]() 或
或![]() (舍去),∴点E的坐标是(2,3),点C′的坐标是(0,1).
(舍去),∴点E的坐标是(2,3),点C′的坐标是(0,1).
综上,可得D点的坐标是(2,9),点E的坐标是(2,3).
(2)如图1所示:
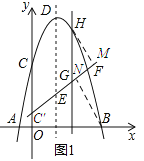
令抛物线![]() 的y=0得:
的y=0得:![]() ,解得:
,解得:![]() ,
,![]() ,所以点A(﹣1,0),B(5,0).设直线C′E的解析式是
,所以点A(﹣1,0),B(5,0).设直线C′E的解析式是![]() ,将E(2,3),C′(0,1),代入得
,将E(2,3),C′(0,1),代入得![]() ,解得:
,解得:![]() ,∴直线C′E的解析式为
,∴直线C′E的解析式为![]() ,联立得:
,联立得: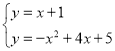 ,解得:
,解得:![]() ,或
,或![]() ,∴点F得坐标为(4,5),点A(﹣1,0)在直线C′E上.∵直线C′E的解析式为
,∴点F得坐标为(4,5),点A(﹣1,0)在直线C′E上.∵直线C′E的解析式为![]() ,∴∠FAB=45°.过点B、H分别作BN⊥AF、HM⊥AF,垂足分别为N、M.∴∠HMN=90°,∠ADN=90°,又∵∠NAD=∠HNM=45°,∴△HGM∽△ABN,∴
,∴∠FAB=45°.过点B、H分别作BN⊥AF、HM⊥AF,垂足分别为N、M.∴∠HMN=90°,∠ADN=90°,又∵∠NAD=∠HNM=45°,∴△HGM∽△ABN,∴![]() ,∵
,∵![]() =5:6,∴
=5:6,∴![]() .∴
.∴![]() ,即
,即![]() ,∴HG=5.设点H的横坐标为m,则点H的纵坐标为
,∴HG=5.设点H的横坐标为m,则点H的纵坐标为![]() ,则点G的坐标为(m,m+1),∴
,则点G的坐标为(m,m+1),∴![]() .解得:
.解得:![]() ,
,![]() ;
;
(3)由平移的规律可知:平移后抛物线的解析式为![]() =
=![]() .将x=5代入
.将x=5代入![]() 得:y=5,∴点T的坐标为(5,5).设直线OT的解析式为
得:y=5,∴点T的坐标为(5,5).设直线OT的解析式为![]() ,将x=5,y=5代入得;k=1,∴直线OT的解析式为
,将x=5,y=5代入得;k=1,∴直线OT的解析式为![]() ,
,
①如图2所示:当PT∥x轴时,△PTQ为等腰直角三角形,
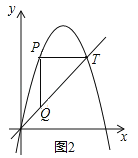
将y=5代入抛物线![]() 得:
得:![]() ,解得:
,解得:![]() ,
,![]() .∴点P的坐标为(1,5).将x=1代入
.∴点P的坐标为(1,5).将x=1代入![]() 得:y=1,∴点Q的坐标为(1,1);
得:y=1,∴点Q的坐标为(1,1);
②如图3所示:
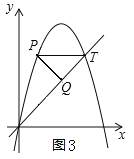
由①可知:点P的坐标为(1,5).∵△PTQ为等腰直角三角形,∴点Q的横坐标为3,将x=3代入![]() 得;y=3,∴点Q得坐标为(3,3);
得;y=3,∴点Q得坐标为(3,3);
③如图4所示:
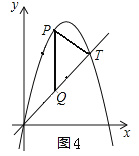
设直线PT解析式为![]() ,∵直线PT⊥QT,∴k=﹣1,将k=﹣1,x=5,y=5代入
,∵直线PT⊥QT,∴k=﹣1,将k=﹣1,x=5,y=5代入![]() 得:b=10,∴直线PT的解析式为
得:b=10,∴直线PT的解析式为![]() .联立得:
.联立得: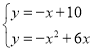 ,解得:
,解得:![]() ,
,![]() ,∴点P的横坐标为2,将x=2代入
,∴点P的横坐标为2,将x=2代入![]() 得,y=2,∴点Q的坐标为(2,2).
得,y=2,∴点Q的坐标为(2,2).
综上所述:点Q的坐标为(1,1)或(3,3)或(2,2).


科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.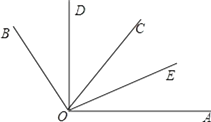
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.
(1)如图1,求证:BD=CE; 
(2)如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°; 
(3)在(2)的条件下,若AD=2BD,FH=9,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图,请你根据图中所给的信息解答下列问题: 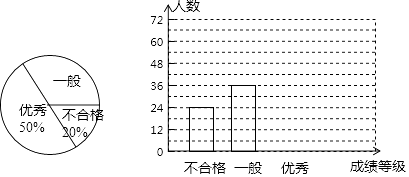
(1)请将下面条形统计图补充完整;
(2)“一般”等级所在扇形的圆心角的度数是度;
(3)若“一般”和“优秀”均被视为达标成绩,该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
(1)求抛物线与x轴的交点坐标;
(2)若点C为抛物线与x轴的交点,是否存在点D,使A、B、C、D四点围成的四边形是平行四边形?若存在,求点D的坐标;若不存在,说明理由;
(3)问几秒钟时,B、D、E在同一条直线上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线l1;y=ax2+bx+c(a<0)经过原点,与x轴的另一个交点为B(4,0),点A为顶点,且直线OA的解析式为y=x.

(1)如图1,求抛物线l1的解析式;
(2)如图2,将抛物线l1绕原点O旋转180°,得到抛物线l2,l2与x轴交于点B′,顶点为A′,点P为抛物线l1上一动点,连接PO交l2于点Q,连接PA、PA′、QA′、QA.
请求:平行四边形PAQA′的面积S与P点横坐标x(2<x≤4)之间的关系式;
(3)在(2)的条件下,如图11﹣3,连接BA′,抛物线l1或l2上是否存在一点H,使得HB=HA′?若存在,请求出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km. 
(1)牧童从A处将牛牵到河边P处饮水后再回到家C,试确定P在何处,所走路程最短?请在图中画出饮水的位置(保留作图痕迹),
不必说明理由.
(2)求出(1)中的最短路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com