
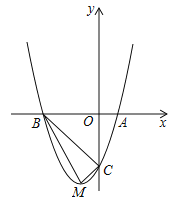
【题目】如图,顶点为M的抛物线![]() 分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)△BCM是直角三角形;(3)N(
;(2)△BCM是直角三角形;(3)N(![]() ,
,![]() )或N(
)或N(![]() ,
,![]() )或N(﹣2,﹣3).
)或N(﹣2,﹣3).
【解析】
试题分析:(1)用待定系数法求出抛物线解析式即可;
(2)由抛物线解析式确定出抛物线的顶点坐标和与x轴的交点坐标,用勾股定理的逆定理即可;
(3)根据题意判断出点N只能在x轴上方的抛物线上,由已知四边形的面积相等转化出S△ABN=S△BCM,然后求出三角形BCM的面积,再建立关于点N的坐标的方程求解即可.
试题解析:(1)∵抛物线![]() 与y轴相交于点C(0,﹣3),∴﹣3=a﹣4,∴a=1,∴抛物线解析式为
与y轴相交于点C(0,﹣3),∴﹣3=a﹣4,∴a=1,∴抛物线解析式为![]() ,即
,即![]() ;
;
(2)△BCM是直角三角形.理由:
由(1)有,抛物线解析式为![]() ,∵顶点为M的抛物线
,∵顶点为M的抛物线![]() ,∴M(﹣1,﹣4),由(1)抛物线解析式为
,∴M(﹣1,﹣4),由(1)抛物线解析式为![]() ,令y=0,∴
,令y=0,∴![]() ,∴
,∴![]() =﹣3,
=﹣3,![]() =1,∴A(1,0),B(﹣3,0),∴
=1,∴A(1,0),B(﹣3,0),∴![]() =9+9=18,
=9+9=18,![]() =1+1=2,
=1+1=2,![]() =4+14=20,∴
=4+14=20,∴![]() ,∴△BCM是直角三角形;
,∴△BCM是直角三角形;
(3)存在.∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,且点M是抛物线的顶点,分两种情况讨论:
①点N在x轴上方的抛物线上,如图,由(2)有△BCM是直角三角形,![]() =18,
=18,![]() =2,∴BC=
=2,∴BC=![]() ,CM=
,CM=![]() ,∴S△BCM=
,∴S△BCM=![]() BC×CM=
BC×CM=![]() =3,设N(m,n),∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,∴S△ABN+S△ABC=S△BCM+S△ABC,∴S△ABN=S△BCM=3,∵A(1,0),B(﹣3,0),∴AB=4,∴S△ABN=
=3,设N(m,n),∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,∴S△ABN+S△ABC=S△BCM+S△ABC,∴S△ABN=S△BCM=3,∵A(1,0),B(﹣3,0),∴AB=4,∴S△ABN=![]() ×AB×n=
×AB×n=![]() ×4×n=2n=3,∴n=
×4×n=2n=3,∴n=![]() ,∵N在抛物线解析式为
,∵N在抛物线解析式为![]() 的图象上,∴
的图象上,∴![]() ,∴m1=
,∴m1=![]() ,m2=
,m2=![]() ,∴N(
,∴N(![]() ,
,![]() )或N(
)或N(![]() ,
,![]() );
);
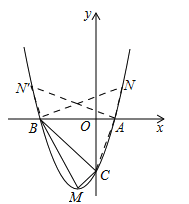
②如图2,点N在x轴下方的抛物线上,∵点C在对称轴的右侧,∴点N在对称轴右侧不存在,只有在对称轴的左侧,过点M作MN∥BC,交抛物线于点N,∵B(﹣3,0),C(0,﹣3),∴直线BC解析式为y=﹣x﹣3,设MN的解析式为y=﹣x+b,∵抛物线解析式为![]() ①,∴M(﹣1,﹣4),∴直线MN解析式为y=﹣x﹣5②,联立①②得:
①,∴M(﹣1,﹣4),∴直线MN解析式为y=﹣x﹣5②,联立①②得: ,解得:
,解得: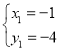 (舍),
(舍),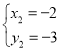 ,∴N(﹣2,﹣3).
,∴N(﹣2,﹣3).
综上所述:N(![]() ,
,![]() )或N(
)或N(![]() ,
,![]() )或N(﹣2,﹣3).
)或N(﹣2,﹣3).



科目:初中数学 来源: 题型:
【题目】设直线l1和直线l2平行,且l1和l2间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A′B′,而A′B′关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系?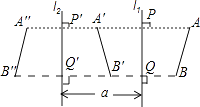
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.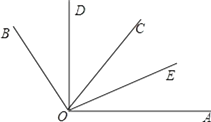
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同.
(1)原计划平均每天生产多少台机器?
(2)若该工厂要在不超过5天的时间,生产1100台机器,则平均每天至少还要再多生产多少台机器?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.
(1)如图1,求证:BD=CE; 
(2)如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°; 
(3)在(2)的条件下,若AD=2BD,FH=9,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线l1;y=ax2+bx+c(a<0)经过原点,与x轴的另一个交点为B(4,0),点A为顶点,且直线OA的解析式为y=x.

(1)如图1,求抛物线l1的解析式;
(2)如图2,将抛物线l1绕原点O旋转180°,得到抛物线l2,l2与x轴交于点B′,顶点为A′,点P为抛物线l1上一动点,连接PO交l2于点Q,连接PA、PA′、QA′、QA.
请求:平行四边形PAQA′的面积S与P点横坐标x(2<x≤4)之间的关系式;
(3)在(2)的条件下,如图11﹣3,连接BA′,抛物线l1或l2上是否存在一点H,使得HB=HA′?若存在,请求出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com