
【题目】计算下列各题:
(1)2(m+1)2﹣(2m+1)(2m﹣1);
(2)4x2﹣(﹣2x+3)(﹣2x﹣3);
(3)先化简,再求值:[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣2,y= ![]() .
.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.
(1)如图1,求证:BD=CE; 
(2)如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°; 
(3)在(2)的条件下,若AD=2BD,FH=9,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
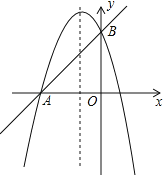
【题目】如图,已知抛物线![]() 与直线AB相交于A(﹣3,0),B(0,3)两点.
与直线AB相交于A(﹣3,0),B(0,3)两点.
(1)求这条抛物线的解析式;
(2)设C是抛物线对称轴上的一动点,求使∠CBA=90°的点C的坐标;
(3)探究在抛物线上是否存在点P,使得△APB的面积等于3?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com