
【题目】如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.

【答案】(1)BE=CD;(2)①成立;②存在,45°或225°.
【解析】
试题分析:(1)由△ABC和△AED都是等腰直角三角形,得到AB=AC,AE=AD,即可得到BE=CD;
(2)①由△ABC和△AED都是等腰直角三角形,得到AB=AC,AE=AD,由旋转的性质可得∠BAE=∠CAD,得到△BAE≌△CAD,根据全等三角形的性质即可得到结论;
②由平行四边形的性质可得∠ABC=∠ADC=45°,再由等腰直角三角形的性质即可得到结论.
试题解析:(1)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,∴AB=AC,AE=AD,∴AE﹣AB=AD﹣AC,∴BE=CD;
(2)①成立,理由如下:
∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,∴AB=AC,AE=AD,由旋转的性质可得∠BAE=∠CAD,在△BAE与△CAD中,∵AB=AC,∠BAE=∠CAD,AE=AD,∴△BAE≌△CAD(SAS),∴BE=CD;
②存在,α=45°.∵以A、B、C、D四点为顶点的四边形是平行四边形,∴∠ABC=∠ADC=45°,∵AC=![]() ED,∴∠CAD=45°,或360°﹣90°﹣45°=225°,∴角α的度数是45°或225°.
ED,∴∠CAD=45°,或360°﹣90°﹣45°=225°,∴角α的度数是45°或225°.



 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
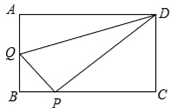
【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证: 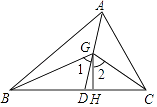
(1)∠BGC=90°+ ![]() ∠BAC;
∠BAC;
(2)∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.
(1)如图1,求证:BD=CE; 
(2)如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°; 
(3)在(2)的条件下,若AD=2BD,FH=9,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图,请你根据图中所给的信息解答下列问题: 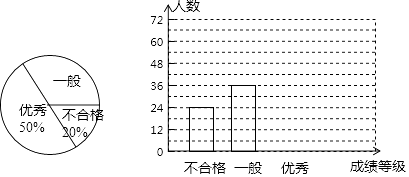
(1)请将下面条形统计图补充完整;
(2)“一般”等级所在扇形的圆心角的度数是度;
(3)若“一般”和“优秀”均被视为达标成绩,该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
(1)求抛物线与x轴的交点坐标;
(2)若点C为抛物线与x轴的交点,是否存在点D,使A、B、C、D四点围成的四边形是平行四边形?若存在,求点D的坐标;若不存在,说明理由;
(3)问几秒钟时,B、D、E在同一条直线上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后,OM恰好平分∠BOC.①求t的值;②此时ON是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠MON?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠MOB?请画图并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com