
【题目】如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证: 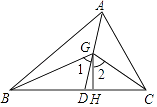
(1)∠BGC=90°+ ![]() ∠BAC;
∠BAC;
(2)∠1=∠2.
【答案】
(1)解:由三角形内角和定理可知:∠ABC+∠ACB=180°﹣∠BAC,
∵BG,CG分别平分∠ABC,∠ACB,
∠GBC= ![]() ∠ABC,∠GCB=
∠ABC,∠GCB= ![]() ∠ACB
∠ACB
∴∠GBC+∠GCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠BAC)=90°﹣
(180°﹣∠BAC)=90°﹣ ![]() ∠BAC
∠BAC
∴∠BGC=180°﹣(∠GBC+∠GCB)=180°﹣ ![]() (∠ABC+∠ACB)=90°+
(∠ABC+∠ACB)=90°+ ![]() ∠BAC;
∠BAC;
(2)解:∵AD是它的角平分线,
∴∠BAD=∠CAD
∴∠1=∠BAD+∠ABG,
∵GH⊥BC,
∴∠GHC=90°
∴∠2=90°﹣∠GCH
=90°﹣ ![]() ∠ACB
∠ACB
=90°﹣ ![]() (180°﹣∠DAC﹣∠ADC)
(180°﹣∠DAC﹣∠ADC)
= ![]() ∠DAC+
∠DAC+ ![]() ∠ADC
∠ADC
∵∠ADC=∠ABC+∠BAD,
∴ ![]() ∠ADC=
∠ADC= ![]() ∠ABC+∠
∠ABC+∠ ![]() ∠BAD
∠BAD
=∠ABG+ ![]() ∠BAD,
∠BAD,
∴∠2= ![]() ∠DAC+
∠DAC+ ![]() ∠ADC
∠ADC
= ![]() ∠BAD+
∠BAD+ ![]() ∠BAD+∠ABG
∠BAD+∠ABG
=∠BAD+∠ABG,
∴∠1=∠2,
【解析】(1)由三角形内角和定理可知∠ABC+∠ACB=180°﹣∠BAC,然后利用角平分线的性质即可求出∠BGC=90°+ ![]() ∠BAC.(2)由于AD是它的角平分线,所以∠BAD=∠CAD,然后根据图形可知:∠1=∠BAD+∠ABG,∠2=90°﹣∠GCH,最后根据三角形的内角和定理以及外角的性质即可求出答案.
∠BAC.(2)由于AD是它的角平分线,所以∠BAD=∠CAD,然后根据图形可知:∠1=∠BAD+∠ABG,∠2=90°﹣∠GCH,最后根据三角形的内角和定理以及外角的性质即可求出答案.
【考点精析】掌握三角形的内角和外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( ) 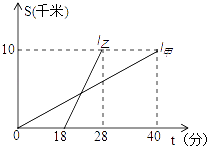
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.

(1)b= ,c= ,点B的坐标为 ;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,符合这一结果的实验可能是( )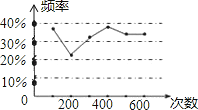
A.掷一枚正六面体的骰子,出现1点的概率
B.任意写一个正整数,它能被3整除的概率
C.抛一枚硬币,出现正面的概率
D.从一个装有2个白球和1个红球的袋子中任取一球,取到白球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
(1)当OC∥AB时,∠BOC的度数为 ;
(2)连接AC,BC,在点C在⊙O运动过程中,△ABC的面积是否存在最大值?并求出△ABC的最大值;
(3)直接写出在(2)的条件下D点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com