
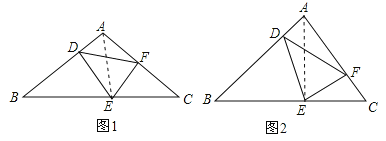
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).

【答案】(1)AB=BE;(2)BD=![]() .
.
【解析】
试题分析:(1)如图1,连结AE.由DE=DF,得到∠DEF=∠DFE,由∠ADF+∠DEC=180°,得到∠ADF=∠DEB.由∠AFE=∠BDE,得到∠AFE+∠ADE=180°,得到A、D、E、F四点共圆,由圆周角定理得出∠DAE=∠DFE=∠DEF,∠ADF=∠AEF.再由∠ADF=∠DEB=∠AEF,得出∠AEF+∠AED=∠DEB+∠AED,则∠AEB=∠DEF=∠BAE,由等角对等边得出AB=BE;
(2)如图2,连结AE.由A、D、E、F四点共圆,得到∠ADF=∠AEF,由∠DAF=90°,得到∠DEF=90°,再证明∠DEB=∠AEF.又∠AFE=∠BDE,得到△BDE∽△AFE,利用相似三角形对应边成比例得到![]() .在Rt△DEF中,利用勾股定理求出EF=
.在Rt△DEF中,利用勾股定理求出EF=![]() DF,然后将AF=m,DE=kDF代入,计算即可求解.
DF,然后将AF=m,DE=kDF代入,计算即可求解.
试题解析:(1)如图1,连结AE.∵DE=DF,∴∠DEF=∠DFE,∵∠ADF+∠DEC=180°,∴∠ADF=∠DEB,∵∠AFE=∠BDE,∴∠AFE+∠ADE=180°,∴A、D、E、F四点共圆,∴∠DAE=∠DFE=∠DEF,∠ADF=∠AEF,∵∠ADF=∠DEB=∠AEF,∴∠AEF+∠AED=∠DEB+∠AED,∴∠AEB=∠DEF=∠BAE,∴AB=BE;
(2)如图2,连结AE.∵∠AFE=∠BDE,∴∠AFE+∠ADE=180°,∴A、D、E、F四点共圆,∴∠ADF=∠AEF,∵∠DAF=90°,∴∠DEF=90°,∵∠ADF+∠DEC=180°,∴∠ADF=∠DEB,∵∠ADF=∠AEF,∴∠DEB=∠AEF,在△BDE与△AFE中,∵∠DEB=∠AEF,∠BDE=∠AFE,∴△BDE∽△AFE,∴![]() ,在直角△DEF中,∵∠DEF=90°,DE=kDF,∴EF=
,在直角△DEF中,∵∠DEF=90°,DE=kDF,∴EF=![]() =
=![]() DF,∴
DF,∴![]() =
=![]() ,∴BD=
,∴BD=![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证: 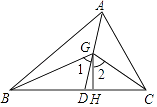
(1)∠BGC=90°+ ![]() ∠BAC;
∠BAC;
(2)∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A. 一组对边平行且相等的四边形是平行四边形
B. 一组对边相等且有一个角是直角的四边形是矩形
C. 一组邻边相等的平行四边形是菱形
D. 一组邻边相等的矩形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2 . 
A.72
B.90
C.108
D.144
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后,OM恰好平分∠BOC.①求t的值;②此时ON是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠MON?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠MOB?请画图并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
某校被调查学生选择社团意向统计表
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |
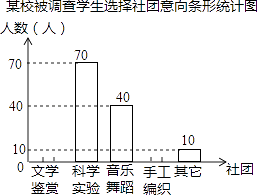
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个学生从点A向北偏东60°方向走40米,到达点B,再从B沿北偏西30°方向走若干米,到达点C,此时恰好在点A的正北方向,则下列说法正确的是( )
A. 点A到BC的距离为30米
B. 点B在点C的南偏东60°方向
C. 点A在点B的南偏西60°方向30米处
D. 以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com