
【题目】如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM,ON分别是∠AOC,∠BOD的平分线,∠MON等于度.
【答案】135
【解析】∵∠AOC=30°,OM是∠AOC的平分线,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() ×30°=15°,
×30°=15°,
∵∠BOD=60°,ON是∠BOD的平分线,
∴∠DON= ![]() ∠BOD=
∠BOD= ![]() ×60°=30°.
×60°=30°.
∵∠AOB是平角,∠AOC=30°,∠BOD=60°,
∴∠COD=∠AOB-∠AOC-∠BOD=180°-30°-60°=90°.
∵∠MOC=15°,∠COD=90°,∠DON=30°,
∴∠MON=∠MOC+∠COD+∠DON=15°+90°+30°=135°.
所以答案是:135°.
【考点精析】根据题目的已知条件,利用角的平分线和角的运算的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式2x2+bx+c分解因式为2(x-3)(x+1),则b,c的值为( ).
A. b=3,c=-1 B. b=-6,c=2
C. b=-6,c=-4 D. b=-4,c=-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知:EG∥AF, , .
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荔枝是岭南一带的特色时令水果.今年5月份荔枝一上市,某水果店的老板用3000元购进了一批荔枝,由于荔枝刚在果园采摘比较新鲜,前两天他以高于进价40% 的价格共卖出150千克,由于荔枝保鲜期短,第三天他发现店里的荔枝卖相已不大好,于是果断地将剩余荔枝以低于进价20%的价格全部售出,前后一共获利750元.
(1)若购进的荔枝为![]() 千克,则这批荔枝的进货价为 ;(用含
千克,则这批荔枝的进货价为 ;(用含![]() 的式子来表示)
的式子来表示)
(2)求该水果店的老板这次购进荔枝多少千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
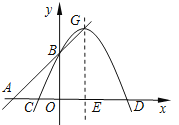
【题目】已知二次函数y=ax2-4ax+a2+2(a<0)图像的顶点G在直线AB上,其中A(![]() ,0)、B(0,3),
,0)、B(0,3),
对称轴与x轴交于点E.
(1)求二次函数y=ax2-4ax+a2+2的关系式;
(2)点P在对称轴右侧的抛物线上,且AP平分四边形GAEP的面积,求点P坐标;
(3)在x轴上方,是否存在整数m,使得当![]() < x ≤
< x ≤![]() 时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com