
【题目】已知二次函数y=ax2-4ax+a2+2(a<0)图像的顶点G在直线AB上,其中A(![]() ,0)、B(0,3),
,0)、B(0,3),
对称轴与x轴交于点E.
(1)求二次函数y=ax2-4ax+a2+2的关系式;
(2)点P在对称轴右侧的抛物线上,且AP平分四边形GAEP的面积,求点P坐标;
(3)在x轴上方,是否存在整数m,使得当![]() < x ≤
< x ≤![]() 时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
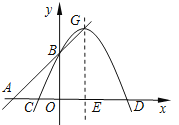
【答案】(1)二次函数关系式为y=-x2+4x+3;
(2)P(![]() ,
, ![]() ),
),
(3)m取-2、-1
【解析】解(1)由A(-![]() ,0)、B(0,3),可设直线AB:y=kx+3,
,0)、B(0,3),可设直线AB:y=kx+3,
从而得,k=2, ∴y=2x+3,
抛物线y=ax2-4ax+a2+2的顶点G(2,a2-4a+2),
点G在直线AB上,∴ a2-4a+2=4+3,∴a=-1,a=5(舍去),
二次函数关系式为y=-x2+4x+3.
(2)∵AP平分四边形GAEP的面积, ∴2S△AEP=S四边形GAEP,
设P(t,-t2+4t+3),
∴ 2×![]() (2+
(2+![]() )(-t2+4t+3)=
)(-t2+4t+3)=![]() ×7×(2+
×7×(2+![]() )+
)+![]() ×7×(t-2)
×7×(t-2)
∴ 2t2-6 t-3=0,∴t1=![]() , t2=
, t2=![]() (舍去)∴P(
(舍去)∴P(![]() ,
, ![]() ),
),
(3)抛物线与x轴交点C(2-![]() ,0),D(2+
,0),D(2+![]() ,0),
,0),
在x轴上方,抛物线y随x增大而减大,则2-![]() <x≤2,
<x≤2,
又∵![]() < x≤
< x≤![]() ,
,
∴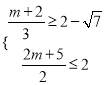 ,得:4-3
,得:4-3![]() ≤m≤-
≤m≤-![]() ,
,
∵整数m为整数,∴m为-3,-2、-1.
又∵![]() <
<![]() ,m>-
,m>-![]() .
.
∴m取-2、-1.


科目:初中数学 来源: 题型:
【题目】某学校为了推动球类运动的普及,成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题: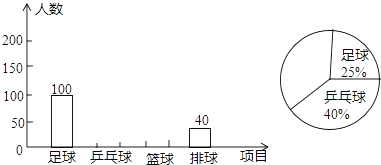
(1)本次抽样调查,共调查了名学生;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1800人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100,那么a1+a2+a3+…a100= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AC上一点,过P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△EPD.(设AP=x)
(1)若点E落在边BC上,求AP的长;
(2)当AP为何值时,△EDB为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为( ).
A.y=x+2
B.y=-x+2
C.y=x+2或y=-x+2
D.y=-x+2或y=x-2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com