
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AC上一点,过P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△EPD.(设AP=x)
(1)若点E落在边BC上,求AP的长;
(2)当AP为何值时,△EDB为等腰三角形.

【答案】(1)AP的长为![]() ;
;
(2)当AP=![]() 、
、![]() 、
、![]() 时,△EDB为等腰三角形.
时,△EDB为等腰三角形.
【解析】解:(1)由题意,∠C=90°,AC=8,BC=6,∴AB=10
∵ AP=DE=x,∴AD=PE=![]() x,PD=
x,PD=![]() x,
x,
点E落在边BC上,PE∥AB,∴![]() =
=![]() ,∴
,∴![]() =
=![]()
∴ x=![]()
(2)∵△EDB为等腰三角形
①若DE=EB(如图)作EM⊥AB于M,则DM=![]() DB=PE=AD=
DB=PE=AD=![]() ,
,
∴![]() x=
x=![]() ,∴ x=
,∴ x=![]() ,∴AP=
,∴AP=![]()
②若BD=DE(如图)
x=10-![]() x,解之x=
x,解之x=![]() ,∴AP=
,∴AP=![]() 。③若BE=BD(如图)
。③若BE=BD(如图)
∵DE∥AC, ∴DE⊥BC,
又∵BE=BD ∴DN=![]() DE=
DE=![]() AP=
AP=![]() x
x
∵Rt△ADP∽Rt△DNB
∴![]() ,∴
,∴ ,∴x=
,∴x=,∴AP=
![]()
综上,当AP=![]() 、
、![]() 、
、![]() 时,
时,
△EDB为等腰三角形.


科目:初中数学 来源: 题型:
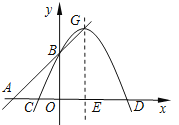
【题目】已知二次函数y=ax2-4ax+a2+2(a<0)图像的顶点G在直线AB上,其中A(![]() ,0)、B(0,3),
,0)、B(0,3),
对称轴与x轴交于点E.
(1)求二次函数y=ax2-4ax+a2+2的关系式;
(2)点P在对称轴右侧的抛物线上,且AP平分四边形GAEP的面积,求点P坐标;
(3)在x轴上方,是否存在整数m,使得当![]() < x ≤
< x ≤![]() 时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数图象经过A(-2,-3),B(1,3)两点.
⑴ 求这个一次函数的解析式.
⑵ 试判断点P(-1,1)是否在这个一次函数的图象上.
⑶ 求此函数与x轴、y轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个暗箱中有大小相同的1只黑球和n只白球(记为白1、白2、…、白n),每次从中取出一只球,取到白球得1分,取到黑球得2分,甲从暗箱中有放回地依次取出2只球,而乙是从暗箱中一次性取出2只球.
(1)若n=2,分别求甲取得3分的概率和乙取得3分的概率;(请用“画树状图”或“列表”等方式给出分析过程)
(2)若乙取得3分的概率小于![]() ,则白球至少有多少个?(请直接写出结果)
,则白球至少有多少个?(请直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com