
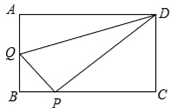
【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
【答案】(1)S=![]() , S不存在最大值,当x=2时,S有最小值,最小值为4;(2)当x=
, S不存在最大值,当x=2时,S有最小值,最小值为4;(2)当x=![]() 时,QP⊥DP.
时,QP⊥DP.
【解析】分析:(1)可用x表示出AQ、BQ、BP、CP,从而可表示出S△ADQ、S△BPQ、S△PCD的面积,则可表示出S,再利用二次函数的增减性可求得是否有最大值,并能求得其最小值;
(2)用x表示出BQ、BP、PC,当QP⊥DP时,可证明△BPQ∽△CDP,利用相似三角形的性质可得到关于x的方程,可求得x的值.
(1)∵四边形ABCD为矩形,∴BC=AD=4,CD=AB=3,当运动x秒时,则AQ=x,BP=x,∴BQ=AB﹣AQ=3﹣x,CP=BC﹣BP=4﹣x,∴S△ADQ=![]() ADAQ=
ADAQ=![]() ×4x=2x,S△BPQ=
×4x=2x,S△BPQ=![]() BQBP=
BQBP=![]() (3﹣x)x=
(3﹣x)x=![]() ,S△PCD=
,S△PCD=![]() PCCD=
PCCD=![]() (4﹣x)3=
(4﹣x)3=![]() ,又S矩形ABCD=ABBC=3×4=12,∴S=S矩形ABCD﹣S△ADQ﹣S△BPQ﹣S△PCD=12﹣2x﹣(
,又S矩形ABCD=ABBC=3×4=12,∴S=S矩形ABCD﹣S△ADQ﹣S△BPQ﹣S△PCD=12﹣2x﹣(![]() )﹣(
)﹣(![]() )=
)=![]() =
=![]() ,即S=
,即S=![]() ,∴S为开口向上的二次函数,且对称轴为x=2,∴当0<x<2时,S随x的增大而减小,当2<x≤3时,S随x的增大而增大,又当x=0时,S=5,当S=3时,S=
,∴S为开口向上的二次函数,且对称轴为x=2,∴当0<x<2时,S随x的增大而减小,当2<x≤3时,S随x的增大而增大,又当x=0时,S=5,当S=3时,S=![]() ,但x的范围内取不到x=0,∴S不存在最大值,当x=2时,S有最小值,最小值为4;
,但x的范围内取不到x=0,∴S不存在最大值,当x=2时,S有最小值,最小值为4;
(2)存在,理由如下:
由(1)可知BQ=3﹣x,BP=x,CP=4﹣x,当QP⊥DP时,则∠BPQ+∠DPC=∠DPC+∠PDC,∴∠BPQ=∠PDC,且∠B=∠C,∴△BPQ∽△PCD,∴![]() ,即
,即![]() ,解得x=
,解得x=![]() (舍去)或x=
(舍去)或x=![]() ,∴当x=
,∴当x=![]() 时,QP⊥DP.
时,QP⊥DP.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC
的顶点在格点上.且A(1,﹣4),B(5,﹣4),C(4,﹣1)
(1)画出△ABC;
(2)求出△ABC的面积;
(3)若把△ABC向上平移2个单位长度,再向左平移
4个单位长度得到△A′B′C′,在图中画出△A′B′C′,并写
出B′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( ) 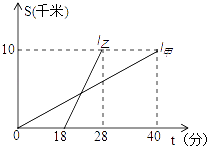
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在边DC的中点E,折痕为AF,已知CD=8cm.求: 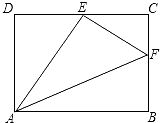
(1)AD的长;
(2)△ABF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博会的某纪念品原价168元,连续两次降价a%后售价为128元.下列所列方程中正确的( )
A.168(1+a%)=128B.168(1-a%)=128
C.168(1-2a%)=128D.168(1+2a%)=128
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com