
����Ŀ����ͼ1��������![]() ��x�ύ�ڵ�A��m��2��0����B��2m+3��0������A�ڵ�B����ࣩ����y�ύ�ڵ�C������BC��
��x�ύ�ڵ�A��m��2��0����B��2m+3��0������A�ڵ�B����ࣩ����y�ύ�ڵ�C������BC��
��1����m��n��ֵ��
��2����ͼ2����NΪ�������ϵ�һ���㣬��λ��ֱ��BC�Ϸ�������CN��BN������NBC��������ֵ��
��3����ͼ3����M��P�ֱ�Ϊ�߶�BC���߶�OB�ϵĶ��㣬����PM��PC���Ƿ���������ĵ�P��ʹ��PCMΪ���������Σ���PMBΪֱ��������ͬʱ�����������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��m=1��n=��9����2��![]() ����3��P��
����3��P��![]() ��0����
��0����![]() ��0����
��0����
��������
�����������1�����������ߵĽ���ʽȷ���Գ���Ϊֱ��x=2�������öԳ��Եõ�2����m��2��=2m+3��2���ⷽ�̿ɵ�m��ֵ���Ӷ��õ�A����1��0����B��5��0����Ȼ���A���������![]() �����n��ֵ��
�����n��ֵ��
��2����ND��y�ύBC��D����ͼ2�����������߽���ʽȷ��C��0��3���������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=��![]() x+3����N��x����
x+3����N��x����![]() x2+
x2+![]() x+3������D��x����
x+3������D��x����![]() x+3�������������������ʽ������S��NBC=S��NDC+S��NDB�ɵ�S��BCN=��
x+3�������������������ʽ������S��NBC=S��NDC+S��NDB�ɵ�S��BCN=��![]() x2+
x2+![]() x��Ȼ�����ö��κ�����������⣻
x��Ȼ�����ö��κ�����������⣻
��3�������ù��ɶ��������BC=![]() ���ٷ������ۣ�����PMB=90�㣬����PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB=
���ٷ������ۣ�����PMB=90�㣬����PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB=![]() ��t��֤����BMP�ס�BOC���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����ꣻ����MPB=90�㣬��MP=MC����PM=t����CM=t��MB=
��t��֤����BMP�ס�BOC���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����ꣻ����MPB=90�㣬��MP=MC����PM=t����CM=t��MB=![]() ��t��֤����BMP�ס�BCO���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����꣮
��t��֤����BMP�ס�BCO���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����꣮
�����������1���������ߵĽ���ʽΪ![]() =
=![]() ���������ߵĶԳ���Ϊֱ��x=2������A�͵�BΪ�ԳƵ㣬��2����m��2��=2m+3��2�����m=1����A����1��0����B��5��0������A����1��0������
���������ߵĶԳ���Ϊֱ��x=2������A�͵�BΪ�ԳƵ㣬��2����m��2��=2m+3��2�����m=1����A����1��0����B��5��0������A����1��0������![]() ��9+n=0�����n=��9��
��9+n=0�����n=��9��
��2����ND��y�ύBC��D����ͼ2�������߽���ʽΪ![]() =
=![]() ����x=0ʱ��y=3����C��0��3������ֱ��BC�Ľ���ʽΪy=kx+b����B��5��0����C��0��3�������
����x=0ʱ��y=3����C��0��3������ֱ��BC�Ľ���ʽΪy=kx+b����B��5��0����C��0��3�������![]() �������
�������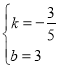 ����ֱ��BC�Ľ���ʽΪ
����ֱ��BC�Ľ���ʽΪ![]() ����N��x��
����N��x��![]() ������D��x��
������D��x��![]() ������ND=
������ND=![]() =
=![]() ����S��NBC=S��NDC+S��NDB=
����S��NBC=S��NDC+S��NDB=![]() 5ND=
5ND=![]() =
=![]() ����x=
����x=![]() ʱ����NBC���������ֵΪ
ʱ����NBC���������ֵΪ![]() ��
��
��3�����ڣ�
��B��5��0����C��0��3������BC=![]() =
=![]() ��������������ۣ�
��������������ۣ�
������PMB=90�㣬����PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB=![]() ��t���ߡ�MBP=��OBC�����BMP�ס�BOC����
��t���ߡ�MBP=��OBC�����BMP�ס�BOC����![]() ����
����![]() �����t=
�����t=![]() ��BP=
��BP=![]() ����OP=OB��BP=5��
����OP=OB��BP=5��![]() =
=![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��0����
��0����
������MPB=90�㣬��MP=MC����PM=t����CM=t��MB=![]() ��t���ߡ�MBP=��CBO�����BMP�ס�BCO����
��t���ߡ�MBP=��CBO�����BMP�ס�BCO����![]() ����
����![]() �����t=
�����t=![]() ��BP=
��BP=![]() ����OP=OB��BP=5��
����OP=OB��BP=5��![]() =
=![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��0����
��0����
����������P��������![]() ��0����
��0����![]() ��0����
��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���Գ���Ϊֱ��x=![]() �������߾���B��2��0����C��0��4�����㣬��������x�����һ����ΪA��
�������߾���B��2��0����C��0��4�����㣬��������x�����һ����ΪA��
��1���������ߵĽ���ʽ��
��2������PΪ��һ�������������ϵ�һ�㣬���ı���COBP�����ΪS����S�����ֵ��
��3����ͼ2����M���߶�BC��һ���㣬��x���Ƿ���������ĵ�Q��ʹ��MQCΪ�����������ҡ�MQBΪֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�͡�A��B��C�����ֱ�߶Գƣ����н����У��١�ABC�ա�A��B��C�䣻
�ڡ�BAC��=��B��AC��
��l��ֱƽ��CC�䣻
��ֱ��BC��B��C��Ľ��㲻һ����l�ϣ�
��ȷ���У� ��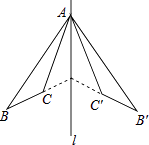
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��l1��ֱ��l2ƽ�У���l1��l2��ľ���Ϊa������߶�AB��l1���Ҳ࣬����AB����l1�ĶԳ�ͼ����A��B�䣬��A��B�����l2�ĶԳ�ͼ����A��B�壨��ͼ������ô���߶�AB��A��B����ʲô��ϵ��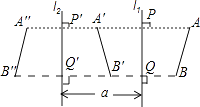
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��B��1��0��
��x�ύ��A��B���㣬��B��1��0��
��1���������ߵĽ���ʽ�͵�A�����ꣻ
��2����ͼ1����P��ֱ��y=x�ϵĶ��㣬��ֱ��y=xƽ�֡�APBʱ�����P�����ꣻ
��3����ͼ2����ֱ֪��![]() �ֱ���x�ᡢy�ύ��C��F���㣬��Q��ֱ��CF�·����������ϵ�һ�����㣬����Q��y���ƽ���ߣ���ֱ��CF�ڵ�D����E���߶�CD���ӳ����ϣ�����QE���ʣ���QDΪ���ĵ�����QDE������Ƿ�������ֵ�������ڣ������������ֵ���������ڣ���˵�����ɣ�
�ֱ���x�ᡢy�ύ��C��F���㣬��Q��ֱ��CF�·����������ϵ�һ�����㣬����Q��y���ƽ���ߣ���ֱ��CF�ڵ�D����E���߶�CD���ӳ����ϣ�����QE���ʣ���QDΪ���ĵ�����QDE������Ƿ�������ֵ�������ڣ������������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
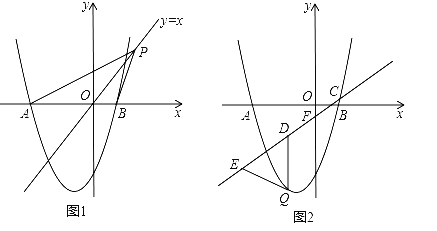
����Ŀ���ھ���ABCD�У�AB=3��AD=4������Q�ӵ�A��������ÿ��1����λ���ٶȣ���AB���B�ƶ���ͬʱ��P�ӵ�B����������ÿ��1����λ���ٶȣ���BC���C�ƶ�������QP��QD��PD����������ͬʱ�˶���ʱ��Ϊx�루0��x��3��������������⣺
��1������QPD�����ΪS���ú�x�ĺ�����ϵʽ��ʾS����xΪ��ֵʱ��S�����ֵ���������Сֵ��
��2���Ƿ����x��ֵ��ʹ��QP��DP����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
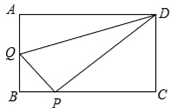
����Ŀ����ͼ��ODƽ�֡�BOC��OEƽ�֡�AOC������BOC=70�㣬��AOC=50�㣮
��1�������AOB���䲹�ǵĶ�����
��2���������DOC�͡�AOE�Ķ��������жϡ�DOE���AOB�Ƿ�����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com