Question

6．如图，在△ABC中，AF=2BF，CE=3AE，CD=4BD．连接CF交DE于P点，求EP：DP的值．

Answer 1

分析 连接EF、DF，根据共高两三角形的底边之比等于面积比可得$\frac{EP}{DP}$=$\frac{{S}_{△CPE}}{{S}_{△CPD}}$=$\frac{{S}_{△FPE}}{{S}_{△FPD}}$，由等比性质可得$\frac{EP}{DP}=\frac{{S}_{△CPE}+{S}_{△FPE}}{{S}_{△CPD}+{S}_{△FPD}}$=$\frac{{S}_{△CEF}}{{S}_{△CDF}}$，再根据AF=2BF、CE=3AE、CD=4BD知$\frac{CE}{AC}=\frac{3}{4}$、$\frac{CD}{BC}=\frac{4}{5}$、$\frac{AF}{AB}=\frac{2}{3}$、$\frac{BF}{AB}=\frac{1}{3}$，从而由$\frac{EP}{DP}$=$\frac{{S}_{△FPE}}{{S}_{△FPD}}$=$\frac{\frac{3}{4}{S}_{△ACF}}{\frac{4}{5}{S}_{△BCF}}$=$\frac{\frac{3}{4}×\frac{2}{3}{S}_{△ABC}}{\frac{4}{5}×\frac{1}{3}{S}_{△ABC}}$可得答案．

解答 解：如图，连接EF、DF，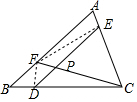

则$\frac{EP}{DP}$=$\frac{{S}_{△CPE}}{{S}_{△CPD}}$=$\frac{{S}_{△FPE}}{{S}_{△FPD}}$，
∵AF=2BF，CE=3AE，CD=4BD，
∴$\frac{CE}{AC}=\frac{3}{4}$，$\frac{CD}{BC}=\frac{4}{5}$，$\frac{AF}{AB}=\frac{2}{3}$，$\frac{BF}{AB}=\frac{1}{3}$，
∴$\frac{EP}{DP}=\frac{{S}_{△CPE}+{S}_{△FPE}}{{S}_{△CPD}+{S}_{△FPD}}$=$\frac{{S}_{△CEF}}{{S}_{△CDF}}$=$\frac{\frac{3}{4}{S}_{△ACF}}{\frac{4}{5}{S}_{△BCF}}$=$\frac{\frac{3}{4}×\frac{2}{3}{S}_{△ABC}}{\frac{4}{5}×\frac{1}{3}{S}_{△ABC}}$=$\frac{15}{8}$．

点评 本题主要考查比例线段的基本性质，根据共高两三角形的底边之比等于面积比将线段的比转化为面积的比是解题的关键．