在Rt△ABC中.∠C=90°.a.b.c分别是∠A.∠B.∠C的对边.若c=15.a:b=3:4.求a.b的长．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

在Rt△ABC中，∠C=90°，a、b、c分别是∠A，∠B，∠C的对边，若c=15，a：b=3：4，求a、b的长．

考点：勾股定理

专题：

分析：设a=BC=3x，b=AC=4x，又其斜边c=AB=15，根据勾股定理即可得出答案．

解答：解：设a=BC=3x，b=AC=4x，又其斜边c=AB=15，
则9x²+16x²=15²，
解得：x=3或-3（舍去），
a=3x=9．
b=4x=12．
故a的长为9，b的长为12．

点评：本题考查了勾股定理的知识，难度不大，注意细心运算即可．勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

在平面直角坐标系中，描出下列各点：A（1，1），B（5，1），C（3，3），D（-3，3），E（-2，2），F（-2，-4），G（5，0），H（3，-4），I（-1，-4），J（3，-2）．
（1）连接AB，CD，EF，GH，IJ，描出它们的中点M、N、P、Q、R，并写出这些中点的坐标；
（2）将上述中点的横坐标和纵坐标分别与对应线段的两个端点的横坐标和纵坐标进行比较，你发现它们之间有什么关系？
（3）根据你的发现，若某线段两端点的坐标分别为（a，b），（c，d），那么该线段的中点坐标为多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

（1）化简：-3（a³b+2b²）+（3a³b-14b²）
（2）化简求值：

（-4x²+2x-8）-（

x-1），其中x=

．

查看答案和解析>>

科目：初中数学 来源： 题型：

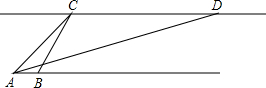有全国最佳深水岸线资源的宁波拥有丰富的海洋资源，为了科学利用海洋资源，发展海洋经济．市政府对A，B两岛屿的海洋资源进行了可持续开发研究．用某勘测飞机测量两岛屿A，B之间的距离．飞机在高空点C处测得岛屿A的俯角∠ECA为45°，岛屿B的俯角∠ECB为60°，然后沿着平行于AB的方向水平飞行了1200海里到点D处，在点D处测得岛屿A的俯角∠EDA为30°，请你根据以上数据，解决下面两个问题：
（1）求飞机的飞行高度；
（2）求两岛屿A、B之间的距离．（结果均保留根号）

查看答案和解析>>

科目：初中数学 来源： 题型：

计算：
（1）2×[5+（-2）³]
（2）90°-18°26′59″．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，AC=AD，BC=BD，求证：AB平分∠CAD．