
【题目】如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,
(1)请判断线段AE和BD的数量关系和位置关系,并证明;
(2)若已知∠AED=135°,设∠AEC=α,当△BDE为等腰三角形时,求α的度数.

【答案】(1)AE=BD且AE⊥BD,理由见解析;(2)当△BDE为等腰三角形时,α的度数为112.5°、135°或90°.
【解析】试题分析:(1)根据![]() 和
和![]() 都是等腰直角三角形、
都是等腰直角三角形、![]() 即可得出
即可得出![]() 再由角的计算即可得出
再由角的计算即可得出![]() 利用全等三角形的判定定理SAS即可证出
利用全等三角形的判定定理SAS即可证出![]() 进而可得出
进而可得出![]() 延长AE,交CD于点H,交BD于点F,根据角的计算即可得出
延长AE,交CD于点H,交BD于点F,根据角的计算即可得出![]() 从而找出
从而找出![]()
(2)根据![]() 是等腰直角三角形即可得出
是等腰直角三角形即可得出![]() 结合
结合![]() 即可找出
即可找出![]() 由
由![]() 可得出
可得出![]() 进而得出
进而得出![]() 再根据三角形内角和定理即可得出
再根据三角形内角和定理即可得出![]() 分
分![]() 以及
以及![]() 三种情况考虑
三种情况考虑![]() 为等腰三角形,代入数据求出
为等腰三角形,代入数据求出![]() 值,此题得解.
值,此题得解.
试题解析:(1)AE=BD且AE⊥BD,理由如下:
∵△ACD和△BCE都是等腰直角三角形, ![]()
∴AC=DC,EC=BC.
![]()
∴∠ACE=∠DCB.
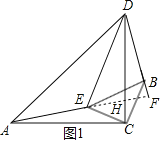
在△ACE和△DCB中, 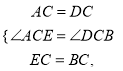
![]()
∴AE=DB,∠CAE=∠CDB.
延长AE,交CD于点H,交BD于点F,如图1所示。
∵∠AHD=∠CHF=∠CDB+∠DFH,∠AHD=∠CAE+∠ACD,
![]()
∴AE⊥BD.
(2)∵△BCE是等腰直角三角形, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
在△DBE中, ![]()
△BDE为等腰三角形分三种情况:
①∠DEB=∠DBE,即![]()
![]()
②∠DEB=∠EDB,即![]()
![]()
③∠DBE=∠EDB,即![]()
![]()
综上所述:当△BDE为等腰三角形时, ![]() 的度数为112.5°、135°或90°.
的度数为112.5°、135°或90°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为______.
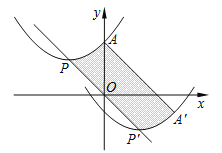
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2![]() ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.
(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年来某县加大了对教育经费的投入,2013年投入2500万元,2015年投入3500万元.假设该县投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是( )
A.2500x2=3500
B.2500(1+x)2=3500
C.2500(1+x%)2=3500
D.2500(1+x)+2500(1+x)2=3500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年底,我国爆发了新一轮的冠状病毒疫情,冠状病毒直径约80-120纳米,1纳米=1.0×10-9米,用科学记数法表示120纳米,其结果是( )
A.1.2×10-9米B.1.2×10-8米C.1.2×10-7米D.1.2×10-6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4)

(1)求B点坐标;
(2)如图2,若C为x正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连接OD,求∠AOD的度数;
(3)如图3,过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式AM=FM+OF是否成立?若成立,请说明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com