
| 树苗 | 每株树批发价格(元) | 两年后每株树苗对空气的净化指数 |
| 杨树 | 3 | 0.4 |
| 柳树 | 2 | 0.1 |
| 樟树 | p | 0.2 |
分析 (1)由三种树苗共购进400株可得出x+x+y=400,变形后即可得出y与x之间的函数关系式;
(2)由这400棵树苗两年后对该住宅小区的空气净化指数不低于90,可得出关于x的一元一次不等式,解之即可得出x的取值范围,设购买树苗的总费用为W,根据总价=单价×数量,即可得出W关于x的函数关系,再根据一次函数的性质可解决最值问题;
(3)根据总价=单价×数量,即可找出W关于x的函数关系.
解答 解:(1)根据题意得:x+x+y=400,
∴y=-2x+400.
(2)根据题意得:0.4x+0.1x+0.2y=0.5x+0.2(-2x+400)≥90,
解得:x≥100;
又∵y≥0,
∴2x≤400,
∴x≤200.
综上可知:100≤x≤200.
设购买树苗的总费用为W,则W=3x+2x+3y=-x+1200,
∵-1<0,
∴W值随x值的增大而减小,
∴当x=200时,W取最小值,最小值为1000.
答:当购买杨树200棵、柳树200棵时,购买树苗的总费用最低,最低费用为1000元.
(3)根据题意得:W=3x+2x+py=5x+(1+0.01x)(-2x+400)=-0.02x2+7x+400.
点评 本题考查了一次函数的应用、一次函数的性质以及一元一次不等式的应用,解题的关键是:(1)根据三种树苗购进总棵数,找出y与x之间的函数关系式;(2)利用一次函数的性质解决最值问题;(3)根据总价=单价×数量,找出W关于x的函数关系.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
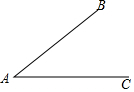 如图,已知∠BAC是一个锐角,在∠BAC所在的平面上任意一点P(P点不在直线AB、AC上)
如图,已知∠BAC是一个锐角,在∠BAC所在的平面上任意一点P(P点不在直线AB、AC上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com