
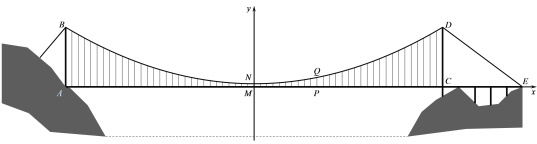
【题目】悬索桥,又名吊桥,指的是以通过索塔悬挂并锚固于两岸(或桥两端)的缆索(或钢链)作为上部结构主要承重构件的桥梁. 其缆索几何形状一般近似于抛物线.从缆索垂下许多吊杆(吊杆垂直于桥面),把桥面吊住.某悬索桥(如图1),是连接两个地区的重要通道. 图2是该悬索桥的示意图.小明在游览该大桥时,被这座雄伟壮观的大桥所吸引. 他通过查找资料了解到此桥的相关信息:这座桥的缆索(即图2中桥上方的曲线)的形状近似于抛物线,两端的索塔在桥面以上部分高度相同,即AB=CD, 两个索塔均与桥面垂直. 主桥AC的长为600 m,引桥CE的长为124 m.缆索最低处的吊杆MN长为3 m,桥面上与点M相距100 m处的吊杆PQ长为13 m.若将缆索的形状视为抛物线,请你根据小明获得的信息,建立适当的平面直角坐标系,求出索塔顶端D与锚点E的距离.


图2
【答案】索塔顶端D与锚点E的距离为155米.
【解析】
先建立适当的平面直角坐标系,AC所在直线为x轴,MN所在直线为y轴,
再由已知条件和抛物线的对称性确定出点坐标:![]() .
.
设抛物线的表达式为![]() .
.
将Q的坐标带入.,解得a的值,就可得出抛物线的表达式.
当MC=![]() 时,带入抛物线的表达式,得出y值就是CD 的长度,在Rt△DCE中利用勾股定理得出DE的长度.
时,带入抛物线的表达式,得出y值就是CD 的长度,在Rt△DCE中利用勾股定理得出DE的长度.
也就是塔顶端D与锚点E的距离
解:如图所示建立平面直角坐标系.
.
依题意可知![]() ,
,
![]() .
.
由抛物线的对称性可知,![]() .则可得点坐标:
.则可得点坐标:![]() .
.
设抛物线的表达式为![]() .
.
因为抛物线经过点Q,
所以将点Q的坐标带入得![]() .
.
解得![]() .
.
得抛物线的表达式为![]() .
.
当![]() 时,得
时,得![]() .
.
因为![]() ,
,
所以![]() .
.
所以![]() .
.
答:索塔顶端D与锚点E的距离为155米.


科目:初中数学 来源: 题型:
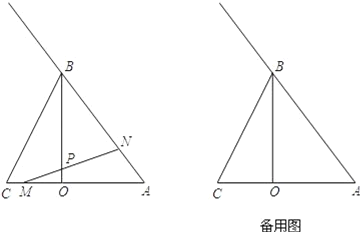
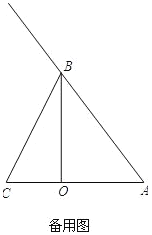
【题目】如图,已知BO是△ABC的AC边上的高,其中BO=8,AO=6,CO=4,点M以2个单位长度/秒的速度自C向A在线段CA上作匀速运动,同时点N以5个单位长度/秒的速度自A向B在射线AB上作匀速运动,MN交OB于点P.当M运动到点A时,点M、N同时停止运动.设点M运动时间为t.
(1)线段AN的取值范围是______.
(2)当0<t<2时,
①求证:MN:NP为定值.
②若△BNP与△MNA相似,求CM的长.
(3)当2<t<5时,若△BNP是等腰三角形,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
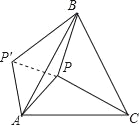
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是关于四个图案的描述.
图1所示是太极图,俗称“阴阳鱼”,该图案关于外圈大圆的圆心中心对称;
图2所示是一个正三角形内接于圆;
图3所示是一个正方形内接于圆;
图4所示是两个同心圆,其中小圆的半径是外圈大圆半径的三分之二.
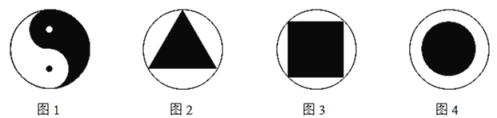
这四个图案中,阴影部分的面积不小于该图案外圈大圆面积一半的是( )
A.图1和图3B.图2和图3C.图2和图4D.图1和图4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.
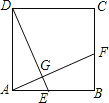
(1)观察图形,写出图中所有与∠AED相等的角.
(2)选择图中与∠AED相等的任意一个角,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c与直线y=﹣3x交于点A,点A横坐标为n﹣1,其中n>1,将OA绕点O逆时针旋转90°后形成OB,点B恰好在抛物线上.
(1)求抛物线的解析式(用含n的代数式表示);
(2)若抛物线与直线y=﹣x+2n﹣5交于C,D两点,且CD=2![]() ,则m值为多少?
,则m值为多少?
(3)若n为整数,当在x轴下方的抛物线上恰好有5个整数点(横坐标为整数),求出n值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com