【题目】甲、乙两个工程队共同承建一段公路路基工程，由乙队先单独施工40天后，甲乙两队共同施工．甲队每天挖土0.425万立方米，乙队工作效率保持不变，设甲、乙两队在此公路施工中的挖土总量
（万立方米）与工作时间
（天）的函数图象如图所示．
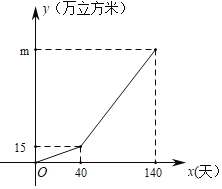
（1）求乙队每天的挖土量；
（2）求此次任务的挖土总量
；
（3）求甲、乙两队共同施工时与之间的函数关系式．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A（0，4）、B（﹣3，0），将线段AB沿x轴正方向平移n个单位得到菱形ABCD．
（1）画出菱形ABCD，并直接写出n的值及点D的坐标；
（2）已知反比例函数y＝
的图象经过点D，ABMN的顶点M在y轴上，N在y＝的图象上，求点M的坐标；
（3）若点A、C、D到某直线l的距离都相等，直接写出满足条件的直线解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】鄂尔多斯市某百货商场销售某一热销商品A，其进货和销售情况如下：用16000元购进一批该热销商品A，上市后很快销售一空，根据市场需求情况，该商场又用7500元购进第二批该商品，已知第二批所购件数是第一批所购件数的一半，且每件商品的进价比第一批的进价少10元．
（1）求商场第二批商品A的进价；
（2）商场同时销售另一种热销商品B，已知商品B的进价与第二批商品A的进价相同，且最初销售价为165元，每天能卖出125件，经市场销售发现，若售价每上涨1元，其每天销售量就减少5件，问商场该如何定售价，每天才能获得最大利润？并求出每天的最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy 中，点A 的坐标为（1，0），P 是第一象限内任意一点，连接PO，PA，若∠POA＝m°，∠PAO＝n°，则我们把（m°，n°）叫做点P 的“双角坐标”.例如，点（1，1）的“双角坐标”为（45°，90°）.若点P到x轴的距离为
，则m+n 的最小值为___．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，二次函数
的图像与坐标轴交于
三点，其中点
的坐标为
，点
的坐标为
，连接
．动点
从点出发，在线段
上以每秒1个单位长度的速度向点
作匀速运动；同时，动点
从点
出发，在线段
上以每秒1个单位长度的速度向点作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为
秒．连接
．
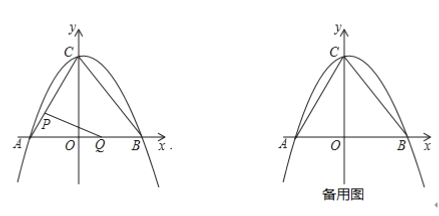
（1）填空：
_________，
________；
（2）在点
运动过程中，
可能是直角三角形吗?请说明理由；
（3）在
轴下方，该二次函数的图象上是否存在点
，使
是以点为直角顶点的等腰直角三角形?若存在，请求出运动时间的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店出售一款商品，商店规定该商品的销售单价不低于68元，经市场调查反映，该商品的日销售量y（件）与销售单价x（元）之间满足一次函数关系，关于该商品的销售单价，日销售量，日销售利润的部分对应数据如下表：[注：日销售利润＝日销售量×（销售单价－成本单价）]
销售单价x（元） | 75 | 78 | 82 |
日销售量y（件） | 150 | 120 | 80 |
日销售利润w（元） | 5250 | 4560 | m |
（1）求y关于x的函数关系式，并直接写出自变量的取值范围；
（2）根据以上信息，
①填空：该产品的成本单价是_______元，表中m的值是______；
②求w关于x的函数关系式；
（3）求该商品日销售利润的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】云岗石窟位于山西大同市，是中国规模最大的古代石窟群之一，位于第五窟的三世佛的中央坐像是云冈石窟最大的佛像．某数学课题研究小组针对“三世佛的中央坐像的高度有多少米”这一问题展开探究，过程如下：
问题提出：
如图①是三世佛的中央坐像，请你设计方案并求出它的高度．
方案设计：
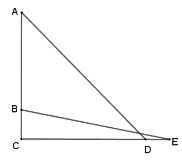
如图②，该课题研究小组通过研究设计了这样一个方案，某同学在
处用测角器测得佛像最高处
的仰角
，另一个同学在他的后方
的
处测得佛像底端
的仰角
．
数据收集：
通过查阅资料和实际测量：佛像底端到观景台的垂直距离
为
．
问题解决：
（1）根据上述方案及数据，求佛像
的高度；（结果保留整数，参考数据：
，
，
，
，
，
）
（2）在实际测量的过程中，有哪些措施可以减小测量数据产生的误差？（写出一条即可）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
