
【题目】云岗石窟位于山西大同市,是中国规模最大的古代石窟群之一,位于第五窟的三世佛的中央坐像是云冈石窟最大的佛像.某数学课题研究小组针对“三世佛的中央坐像的高度有多少米”这一问题展开探究,过程如下:

问题提出:
如图①是三世佛的中央坐像,请你设计方案并求出它的高度.
方案设计:
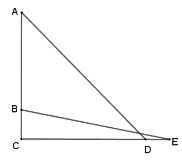
如图②,该课题研究小组通过研究设计了这样一个方案,某同学在![]() 处用测角器测得佛像最高处
处用测角器测得佛像最高处![]() 的仰角
的仰角![]() ,另一个同学在他的后方
,另一个同学在他的后方![]() 的
的![]() 处测得佛像底端
处测得佛像底端![]() 的仰角
的仰角![]() .
.
数据收集:
通过查阅资料和实际测量:佛像底端到观景台的垂直距离![]() 为
为![]() .
.
问题解决:
(1)根据上述方案及数据,求佛像![]() 的高度;(结果保留整数,参考数据:
的高度;(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(2)在实际测量的过程中,有哪些措施可以减小测量数据产生的误差?(写出一条即可)
【答案】(1)![]() ;(2)答案不唯一,详见解析
;(2)答案不唯一,详见解析
【解析】
(1)先由tan∠BEC=![]() 求出CE=
求出CE=![]() ≈27.78,据此得出CD的长,再由tan∠ADC=
≈27.78,据此得出CD的长,再由tan∠ADC=![]() 得AC=CDtan∠ADC,根据AB=AC-BC可得答案;
得AC=CDtan∠ADC,根据AB=AC-BC可得答案;
(2)答案不唯一.例:多次测量求取平均值;两次测量仰角时,应保持观测点及两名测量人员始终在同一直线上等.
(1)在Rt△BCE中,∵tan∠BEC=![]() ,∠BEC=10°,BC=5,
,∠BEC=10°,BC=5,
∴CE=![]() ≈27.78(m),
≈27.78(m),
∵DE=2.14m,
∴CD=CE-DE=27.78-2.14=25.64(m),
在Rt△ACD中,∵tan∠ADC=![]() ,
,
∴AC=CDtan∠ADC=25.64×tan40°≈21.5(m),
则AB=AC-BC=21.5-5≈17(m),
答:佛像AB的高度约为17m;
(2)答案不唯一.例:多次测量求取平均值;两次测量仰角时,应保持观测点及两名测量人员始终在同一直线上等.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】下面是小元设计的“过直线外一点作已知直线的平行线”的尺规作图过程.

已知:如图,直线l和直线外一点P.
求作:过点P作直线l的平行线.
作法:如图,
①在直线l上任取点O;
②作直线![]() ;
;
③以点O为圆心![]() 长为半径画圆,交直线
长为半径画圆,交直线![]() 于点A,交直线l于点B;
于点A,交直线l于点B;
④连接![]() ,以点B为圆心,
,以点B为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点C(点A与C不重合);
于点C(点A与C不重合);
⑤作直线![]() .
.
则直线![]() 即为所求.
即为所求.
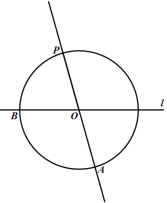
根据小元设计的尺规作图过程,完成以下任务.
(1)补全图形;
(2)完成下面的证明:
证明:连接![]()
∵![]()
∴![]()
∴![]() _______
_______![]() _________,
_________,
又∵![]() ,
,
∴![]() _______
_______![]() _________,
_________,
∴![]() ,
,
∴![]() (___________________________)(填推理的依据).
(___________________________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条长为600m的笔直道路上均匀地跑步,速度分别为![]() 和
和![]() ,起跑前乙在起点,甲在乙前面50m处,若两人同时起跑,则从起跑出发到其中一人先到达终点的过程中,两人之间的距离y(m)与时间t(s)的函数图象是( )
,起跑前乙在起点,甲在乙前面50m处,若两人同时起跑,则从起跑出发到其中一人先到达终点的过程中,两人之间的距离y(m)与时间t(s)的函数图象是( )
A.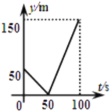 B.
B.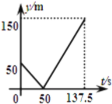 C.
C.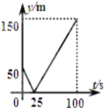 D.
D.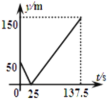
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,矩形ABCD的对角线长为a,对角线与一边的夹角为α(α≤45°),则CD= (用α的三角函数和a来表示),S△BCD= (用α的三角函数和a来表示)= (用2α的三角函数和a来表示);
(2)猜想并直接写出sin2α,sinα,cosα之间的数量关系.
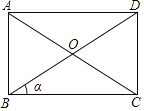
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点![]() )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点
)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点![]() )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点
)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点![]() )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )

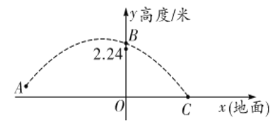
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
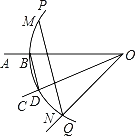
【题目】如图:已知锐角∠AOC,依次按照以下顺序操作画图:
(1)在射线OA上取一点B,以点O为圆心,OB长为半径作![]() ,交射线OC于点D,连接BD;
,交射线OC于点D,连接BD;
(2)分别以点B,D为圆心,BD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接ON,MN.
根据以上作图过程及所作图形可知下列结论:①OC平分∠AON;②MN∥BD;③MN=3BD;④若∠AOC=30°,则MN=![]() ON.其中正确结论的序号是_____.
ON.其中正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
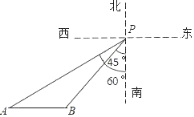
【题目】在某海域,一艘海监船在P处检测到南偏西45°方向的B处有一艘不明船只,正沿正西方向航行,海监船立即沿南偏西60°方向以40海里/小时的速度去截获不明船只,经过1.5小时,刚好在A处截获不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数).
≈1.73,结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
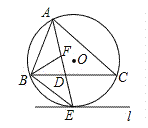
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com