
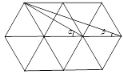
【题目】如图,由10个完全相同的正三角形构成的网格图中,![]() 如图所示,则
如图所示,则![]() =______.
=______.
【答案】![]() .
.
【解析】
给图中各点标上字母,连接DE,利用等腰三角形的性质及三角形内角和定理可得出∠α=30°,同理,可得出:∠CDE=∠CED=30°=∠α,由∠AEC=60°结合∠AED=∠AEC+∠CED可得出∠AED=90°,设等边三角形的边长为a,则AE=2a,DE=![]() a,利用勾股定理可得出AD的长,再结合余弦的定义即可求出cos(α+β)的值.
a,利用勾股定理可得出AD的长,再结合余弦的定义即可求出cos(α+β)的值.
给图中各点标上字母,连接DE,如图所示.
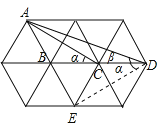
在△ABC中,∠ABC=120°,BA=BC,
∴∠α=30°.
同理,可得出:∠CDE=∠CED=30°=∠α.
又∵∠AEC=60°,
∴∠AED=∠AEC+∠CED=90°.
设等边三角形的边长为a,则AE=2a,DE=2×sin60°a=![]() a,
a,
∴![]() ,
,
∴cos(α+β)=![]() .
.
故答案为:![]() .
.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
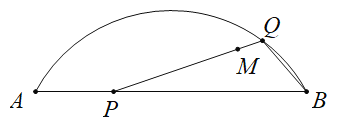
【题目】如图,M是弦![]() 与弧
与弧![]() 所围成的图形的内部的一个定点,P是弦
所围成的图形的内部的一个定点,P是弦![]() 上一动点,连接
上一动点,连接![]() 并延长交弧
并延长交弧![]() 于点Q,连接
于点Q,连接![]() .
.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,P,Q两点间距离为
,P,Q两点间距离为![]() ,
,![]() 两点间距离为
两点间距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值,补全下表:
与x的几组对应值,补全下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.24 | 4.24 | 3.24 | 1.54 | 1.79 | 3.47 | |
| 1.31 | 1.34 | 1.42 | 1.54 | 1.80 | 2.45 | 3.47 |
(2)在同一平面直角坐标系![]() 中,描出表中各组数值对应的点
中,描出表中各组数值对应的点![]() 和
和![]() 并画出函数
并画出函数![]() 的图象;
的图象;
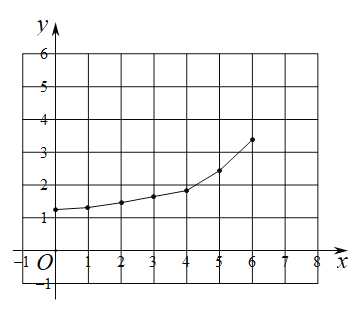
(3)结合函数图象,解决问题:当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约_________
的长度约_________![]() .(精确到0.1)
.(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
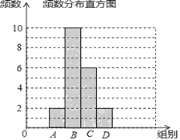
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
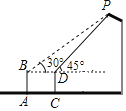
【题目】小明同学在数学实践活动课中测景路灯的高度,如图,已知她的目高AB为1.5米,街为站在A处看路灯顶端P的仰角为30°.再往前走2米站在C处,看路灯顶端P的仰角为45°,求路灯顶端P到地面的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云岗石窟位于山西大同市,是中国规模最大的古代石窟群之一,位于第五窟的三世佛的中央坐像是云冈石窟最大的佛像.某数学课题研究小组针对“三世佛的中央坐像的高度有多少米”这一问题展开探究,过程如下:

问题提出:
如图①是三世佛的中央坐像,请你设计方案并求出它的高度.
方案设计:
如图②,该课题研究小组通过研究设计了这样一个方案,某同学在![]() 处用测角器测得佛像最高处
处用测角器测得佛像最高处![]() 的仰角
的仰角![]() ,另一个同学在他的后方
,另一个同学在他的后方![]() 的
的![]() 处测得佛像底端
处测得佛像底端![]() 的仰角
的仰角![]() .
.
数据收集:
通过查阅资料和实际测量:佛像底端到观景台的垂直距离![]() 为
为![]() .
.
问题解决:
(1)根据上述方案及数据,求佛像![]() 的高度;(结果保留整数,参考数据:
的高度;(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(2)在实际测量的过程中,有哪些措施可以减小测量数据产生的误差?(写出一条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 和点
和点![]() 两点.
两点.
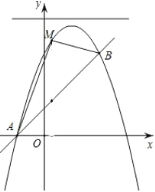
⑴求抛物线![]() 的函数表达式;
的函数表达式;
⑵若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,以
上方抛物线上的一动点,以![]() 为相邻两边作平行四边形
为相邻两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时四边形
的面积最大时,求此时四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
⑶在抛物线![]() 的对称轴上是否存在定点
的对称轴上是否存在定点![]() ,使抛物线
,使抛物线![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,若存在,求出定点
的距离,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
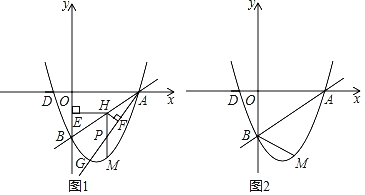
【题目】如图,一次函数y=![]() x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
(1)求二次函数的解析式;
(2)如图1,已知点G(1,m)在抛物线上,作射线AG,点H为线段AB上一点,过点H作HE⊥y轴于点E,过点H作HF⊥AG于点F,过点H作HM∥y轴交AG于点P,交抛物线于点M,当HEHF的值最大时,求HM的长;
(3)在(2)的条件下,连接BM,若点N为抛物线上一点,且满足∠BMN=∠BAO,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com