
分析 先针对于22的3个正约数,对于32的3个正约数,对于42的5个正约数,对于52的3个正约数,对于62的9个正约数分别计算,找出n2的正约数的个数的规律(如果n2分解质因数为ae×bf×ch,那么正约数的个数为(e+1)(f+1)(h+1),和所求结论的规律则$\frac{1}{{d}_{1}+n}$+$\frac{1}{{d}_{2}+n}$+$\frac{1}{{d}_{3}+n}$+…+$\frac{1}{{d}_{m}+n}$=$\frac{m}{2n}$,规律,即可得出结论.
解答 解:对于22的(2+1)=3个正约数1,2,22,有$\frac{1}{1+2}$+$\frac{1}{2+2}$+$\frac{1}{{2}^{2}+2}$=$\frac{3}{4}$;
对于32的(2+1)=3个正约数1,3,32,有$\frac{1}{1+3}$+$\frac{1}{3+3}$+$\frac{1}{{3}^{2}+3}$=$\frac{1}{2}$=$\frac{3}{6}$;
对于42=24的(4+1)-5个正约数1,2,22,23,24,有$\frac{1}{1+4}$+$\frac{1}{2+4}$+$\frac{1}{{2}^{2}+4}$+$\frac{1}{{2}^{3}+4}$+$\frac{1}{{2}^{4}+4}$=$\frac{5}{8}$.
对于52的(2+1)=3个正约数1,5,52,有$\frac{1}{1+5}$+$\frac{1}{5+5}$+$\frac{1}{{5}^{2}+5}$=$\frac{3}{10}$,
对于62=22×32的(2+1)(2+1)=9个正约数1,2,22,3,32,2×3,22×3,2×32,22×32,
有$\frac{1}{1+6}$+$\frac{1}{2+6}$+$\frac{1}{{2}^{2}+6}$+$\frac{1}{3+6}$+$\frac{1}{{3}^{2}+6}$+$\frac{1}{2×3+6}$+$\frac{1}{{2}^{2}×3+6}$+$\frac{1}{2×{3}^{2}+6}$+$\frac{1}{{2}^{2}×{3}^{2}+6}$=$\frac{9}{12}$,
…
…
即:若n2的所有正约数为d1,d2,d3,d4,…,dm,则$\frac{1}{{d}_{1}+n}$+$\frac{1}{{d}_{2}+n}$+$\frac{1}{{d}_{3}+n}$+…+$\frac{1}{{d}_{m}+n}$=$\frac{m}{2n}$
∵20162=210×34×72
∴m=(10+1)(4+1)(2+1)=m=165,
∴当n=2016时,$\frac{1}{{d}_{1}+2016}$+$\frac{1}{{d}_{2}+2016}$+…+$\frac{1}{{d}_{m}+2016}$=$\frac{165}{2×2016}$=$\frac{165}{4032}$,
故答案为$\frac{165}{4032}$.
点评 此题是约数与倍数,主要考查了一个正整数的平方的正约数的确定,以及正约数的个数的确定,找出规律是解本题的关键,也是难点.是一道比较难度比较大的规律题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
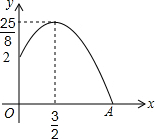 某公园有一喷水池,已知喷水管高2m,喷水最高高度为$\frac{25}{8}$m,此时喷水的水平距离为$\frac{3}{2}$m,求圆形水池的半径.
某公园有一喷水池,已知喷水管高2m,喷水最高高度为$\frac{25}{8}$m,此时喷水的水平距离为$\frac{3}{2}$m,求圆形水池的半径.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com