
分析 (1)由绝对值的非负性得:a+4=0,由偶次方的非负性得:b-3=0,解出并画数轴;
(2)先根据数轴上两点的距离表示出BM和AM的长,再分三种情况进行讨论::①当点M在点B的右侧,②当点M在点A与B之间时,③当点M在点A的左侧时;代入计算即可;
(3)①分别表示出A、B、M三点表示的数,向左减,向右加;
②同理按(2)分三种情况计算.
解答 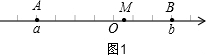 解:(1)如图1,由题意得:a+4=0,b-3=0,
解:(1)如图1,由题意得:a+4=0,b-3=0,
则a=-4,b=3;
(2)线段BM与AM的差即BM-AM的值发生变化,理由是:
设点M对应的数为c,
由BM=|c-b|,AM=|c-a|,
则分三种情况:①当点M在点B的右侧时,如图2,BM-AM=c-b-c+a=a-b=-4-3=-7,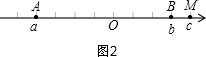
②当点M在点A与B之间时,BM-AM=b-c-c+a=a+b-2c=-4+3-2c=-1-2c,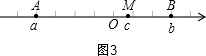
③当点M在点A的左侧时,BM-AM=b-c-a+c=b-a=3+4=7,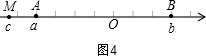
(3)①点A表示的数为:-4-tx;点B表示的数为:3+yt;点M表示的数为:y-tx;
②线段BM与AM的差即BM-AM的值一定发生变化,理由是:
分三种情况:
i)当点M在点B的右侧时,如图2,BM-AM=-AB=-(3+yt+4+tx)=-7-yt-tx,
ii)当点M在点A与B之间时,如图3,BM-AM=3+yt-y+tx-(y-tx+4+tx)=-1-2y+tx+yt,
iii)当点M在点A的左侧时,BM-AM=AB=3+yt+4+tx=7+yt+tx.
点评 本题考查了数轴及绝对值与偶次方的非负性,掌握数轴上两点的距离公式:若点A表示a,点B表示b时,AB=|xb-xa|,同时如果出现几个非负数的和为零时,则令每个非负数为零,列方程计算即可.


科目:初中数学 来源: 题型:解答题
 我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:| 成绩段 | 频数 | 频率 |
| 160≤x<170 | 5 | 0.1 |
| 170≤x<180 | 10 | a |
| 180≤x<190 | b | 0.14 |
| 190≤x<200 | 16 | c |
| 200≤x<210 | 12 | 0.24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD的对角线AC与BD相交于点M,矩形MNPQ与矩形ABCD全等,射线MN与MQ分别交BC边于E、F两点,若AB=2,求证:$\frac{1}{M{E}^{2}}$+$\frac{1}{M{F}^{2}}$=1.
如图,矩形ABCD的对角线AC与BD相交于点M,矩形MNPQ与矩形ABCD全等,射线MN与MQ分别交BC边于E、F两点,若AB=2,求证:$\frac{1}{M{E}^{2}}$+$\frac{1}{M{F}^{2}}$=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com