Question

16．在平面直角坐标系中，点A的坐标为（m，n），若点A′（m，n′）的纵坐标满足n′=$\left\{\begin{array}{l}m-n（m≥n）\\ n-m（n＞m）\end{array}$，则称点A′是点A的“绝对点”．
（1）点（1，2）的“绝对点”的坐标为（1，1）．
（2）点P是函数y=$\frac{2}{x}$的图象上的一点，点P′是点P的“绝对点”．若点P与点P′重合，求点P的坐标．
（3）点Q（a，b）的“绝对点”Q′是函数y=2x²的图象上的一点．当0≤a≤2 时，求线段QQ′的最大值．

Answer 1

分析 （1）根据“绝对点”的定义求解可得；
（2）设点P的坐标为（m，n）．若m≥n，则P′的坐标为（m，m-n），根据P与P′重合知n=m-n，由mn=2求得m、n的值可得；若m＜n，则P′的坐标为（m，n-m）．可得m=0，舍去；
（3）当a≥b时，Q′的坐标为（a，a-b），由Q′是函数y=2x²的图象上一点知a-b=2a²，即b=a-2a ²．可得QQ′=|a-b-b|=|a-2（a-2a²）|=|4a²-a|，利用二次函数的图象和性质求出其最大值；当a＜b时，Q′的坐标为（a，b-a），知QQ′=|b-b+a|=|a|，显然可得其最值．

解答 解：（1）∵2＞1，
∴点（1，2）的“绝对点”的纵坐标为2-1=1，
则点（1，2）的“绝对点”的坐标为（1，1），
故答案为：（1，1）． 

（2）设点P的坐标为（m，n）．
当m≥n时，P′的坐标为（m，m-n）．
若P与P′重合，则n=m-n，
又mn=2．
所以n=±1．
即P的坐标为（2，1）或（-2，-1）．
又（-2，-1）不符合题意，舍去，
所以P的坐标为（2，1）．
当m＜n时，P′的坐标为（m，n-m）．可得m=0，舍去．
综上所述，点P的坐标为（2，1）．

（3）当a≥b时，Q′的坐标为（a，a-b）．
因为Q′是函数y=2x²的图象上一点，
所以a-b=2a²．
即b=a-2a ²．
QQ′=|a-b-b|=|a-2（a-2a²）|=|4a²-a|，
其函数图象如图所示：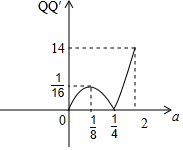
．
由图象可知，当a=2时，QQ′的最大值为14．
当a＜b时，Q′的坐标为（a，b-a）．
QQ′=|b-b+a|=|a|．
当a=2时，QQ′的最大值为2．
综上所述，Q Q′的最大值为14或2．

点评 本题主要考查二次函数的综合应用，理解“绝对点”的定义及二次函数的图象和性质、两点间的距离公式是解题的关键．