
 如图,正五边形ABCDE中.
如图,正五边形ABCDE中.分析 (1)只要证明△APB∽△ABC,可得$\frac{AP}{AB}$=$\frac{AB}{AC}$,由此即可解决问题;
(2)由(1)可知,∠CBP=∠CPB=72°,推出AB=BC=PC,设AB=BC=PC=x,则有x2=2(2-x),解方程即可;
(3)如图3中,延长BE交CN的延长线于F,延长CE交BM的延长线于G.易知BE=CE=$\frac{\sqrt{5}+1}{2}$AB,设AB=a,则BE=CE=$\frac{\sqrt{5}+1}{2}$a.由CD∥BF,AB∥CG,推出$\frac{DC}{EF}$=$\frac{DN}{NE}$=1,推出EF=CD=a,推出$\frac{ME}{AM}$=$\frac{EG}{AB}$,由CF∥BG,可得$\frac{EG}{EC}$=$\frac{BE}{EF}$=$\frac{\sqrt{5}+1}{2}$,推出$\frac{EG}{\frac{\sqrt{5}+1}{2}AB}$=$\frac{\sqrt{5}+1}{2}$,推出$\frac{EG}{AB}$=$\frac{3+\sqrt{5}}{2}$,由此即可解决问题;
解答 (1)证明:如图1中,
∵ABCDE是正五边形,
∴AE=AB=BC,∠BAE=∠ABC=108°,
∴∠ABE=∠AEB=∠ACB=∠BAC=36°,
∵∠BAP=∠BAC,∠ABP=∠ACB,
∴△APB∽△ABC,
∴$\frac{AP}{AB}$=$\frac{AB}{AC}$,
∴AB2=AP•AC.
(2)解:如图1中,
由(1)可知,∠CBP=∠CPB=72°,
∴AB=BC=PC,设AB=BC=PC=x,
则有x2=2(2-x),
解得x=$\sqrt{5}$-1或-$\sqrt{5}$-1(舍弃),
∴AB=$\sqrt{5}$-1.
(3)解:如图3中,延长BE交CN的延长线于F,延长CE交BM的延长线于G.
易知BE=CE=$\frac{\sqrt{5}+1}{2}$AB,设AB=a,则BE=CE=$\frac{\sqrt{5}+1}{2}$a.
∵CD∥BF,AB∥CG,
∴$\frac{DC}{EF}$=$\frac{DN}{NE}$=1,
∴EF=CD=a,
∴$\frac{ME}{AM}$=$\frac{EG}{AB}$,
∵CF∥BG,
∴$\frac{EG}{EC}$=$\frac{BE}{EF}$=$\frac{\sqrt{5}+1}{2}$,
∴$\frac{EG}{\frac{\sqrt{5}+1}{2}AB}$=$\frac{\sqrt{5}+1}{2}$,
∴$\frac{EG}{AB}$=$\frac{3+\sqrt{5}}{2}$,
∴$\frac{ME}{AM}$=$\frac{EG}{AB}$=$\frac{3+\sqrt{5}}{2}$.
点评 本题考查四边形综合题、相似三角形的判定和性质、一元二次方程、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,学会利用参数,构建方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
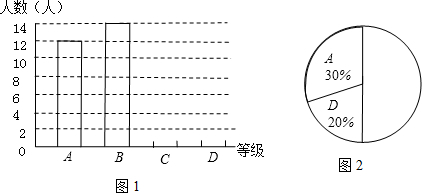
| 等级 | 一分钟跳 绳次数x | 人数 |
| A | x>180 | 12 |
| B | 150<x≤180 | 14 |
| C | 120<x≤150 | a |
| D | x≤120 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )| A. | 32° | B. | 64° | C. | 77° | D. | 87° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 ”组成,其中第①个图案中有4个,第②个图案中有9个,第③个图案中有16个,第④个图案有25个,…,则第⑨个图案中的个数为( )
”组成,其中第①个图案中有4个,第②个图案中有9个,第③个图案中有16个,第④个图案有25个,…,则第⑨个图案中的个数为( )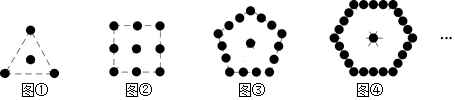
| A. | 90 | B. | 99 | C. | 100 | D. | 111 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com