
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当点P运动到CD上时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

【答案】(1)(-2,0);(2)①t=2;②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);③能确定,z=x+y.
【解析】
(1)根据平移的性质即可得到结论;
(2)①由点C的坐标为(-3,2).得到BC=3,CD=2,由于点P的横坐标与纵坐标互为相反数;于是确定点P在线段BC上,有PB=CD,即可得到结果;
②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);
③如图,过P作PF∥BC交AB于F,则PF∥AD,根据平行线的性质即可得到结论.
解:(1)根据题意,可得
三角形OAB沿x轴负方向平移3个单位得到三角形DEC,
∵点A的坐标是(1,0),
∴点E的坐标是(-2,0);
故答案为:(-2,0);
(2)①∵点C的坐标为(-3,2)
∴BC=3,CD=2,
∵点P的横坐标与纵坐标互为相反数;
∴点P在线段BC上,
∴PB=CD,
即t=2;
∴当t=2秒时,点P的横坐标与纵坐标互为相反数;
故答案为:2;
②当点P在线段BC上时,点P的坐标(-t,2),
当点P在线段CD上时,点P的坐标(-3,5-t);
③能确定,
如图,过P作PF∥BC交AB于F,
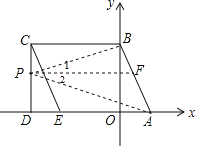
则PF∥AD,
∴∠1=∠CBP=x°,∠2=∠DAP=y°,
∴∠BPA=∠1+∠2=x°+y°=z°,
∴z=x+y.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得y=![]() =4-
=4-![]() x,(x、y为正整数)
x,(x、y为正整数)
∴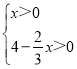 则有0<x<6
则有0<x<6
又y=4-![]() x为正整数,则
x为正整数,则![]() x为正整数.
x为正整数.
从而x=3,代入y=4-![]() ×3=2
×3=2
∴2x+3y=12的正整数解为![]() .
.
利用以上方法解决下列问题:
七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2 其中正确结论的个数是( )
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2 其中正确结论的个数是( )

A. 1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.

解:∵EF∥AD(已知)
∴∠2=_________( )
∵∠1=∠2(已知)
∴∠1=__________( )
∴DG∥BA ( )
又∵∠BAC=70°(已知)
∴∠AGD=_________°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在以AB为直径的半圆内,连接AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法一定正确的是( )
①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.

A. ①③ B. ①④ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线ll,l2交于点O,点P关于ll,l2的对称点分别为P1、P2.
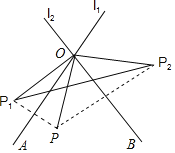
(1)若ll,l2相交所成的锐角∠AOB=60°,则∠P1OP2=______;
(2)若OP=3,P1P2=5,求△P1OP2的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.
![]() ;
; ![]() ;
; ![]() ;
;
(3)求出△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D,C两点分别落在点D′,C′的位置,∠DEF=∠D′EF,并利用量角器量得∠EFB=66°,则∠AED′的度数为( )

A. 66°B. 132°C. 48°D. 38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司技术人员用“沿直线AB折叠检验塑胶带两条边缘线a、b是否互相平行”.
(1)如图1,测得∠1=∠2,可判定a∥b吗?请说明理由;
(2)如图2,测得∠1=∠2,且∠3=∠4,可判定a∥b吗?请说明理由;
(3)如图3,若要使a∥b,则∠1与∠2应该满足什么关系式?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com