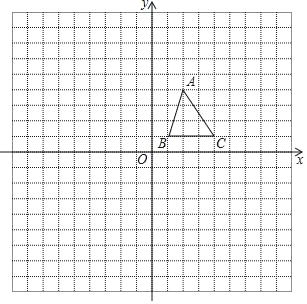
【题目】△ABC在平面直角坐标系中的位置如图所示（坐标系内正方形网格的单位长度为1）：
（1）在网格内画出和△ABC以点O为位似中心的位似图形△A1B1C1，使△A1B1C1和△ABC的位似比为2：1且△A1B1C1位于y轴左侧；
（2）分别写出A1、B1、C1三个点的坐标：A1 、B1 、C1 ；
（3）求△A1B1C1的面积为 ．
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，A、B两点分别在x轴、y轴上，OA=3，OB=4，连结AB．点P在平面内，若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合)，则满足条件的点P有_______个．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD是平行四边形，从下列条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中，再选两个做为补充，使ABCD变为正方形．下面四种组合，错误的是（ ）
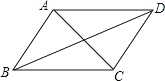
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司员工分别住在
三个住宅区，
区有
人，
区有
人，
区有
人．三个区在一条直线上，位置如图所示．公司的接送打算在此间只设一个停靠点，要使所有员工步行到停靠点的路程总和最少，那么停靠点的位置应在（ ）
A.区B.区C.区D.不确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在
中，
是直角，
，
、
分别是
、
的平分线，、相交于点
．
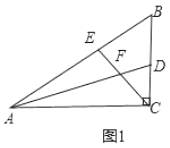
（1）求出
的度数；
（2）判断
与
之间的数量关系并说明理由．（提示：在
上截取
，连接
．）
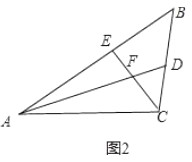
（3）如图2，在△中，如果不是直角，而（1）中的其它条件不变，试判断线段
、
与之间的数量关系并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C=90°，CD⊥AB于D．已知AB=13，CD=6，则Rt△ABC的周长为（ ）
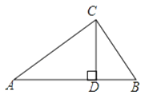
A. 13+5
B. 13+13 C. 13+9
D. 18
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了探索代数式
的最小值，
小张巧妙的运用了数学思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作
，连结AC、EC．已知AB=1，DE=5，BD=8，设BC=x．则
，
则问题即转化成求AC+CE的最小值．
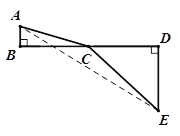
(1)我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得的最小值等于 ，此时x= ；
(2)题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想；
(选填：函数思想，分类讨论思想、类比思想、数形结合思想)
(3)请你根据上述的方法和结论，试构图求出代数式
的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
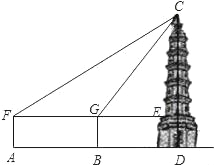
【题目】在一次数学活动课上，老师带领同学们区测量一座古塔CD的高度，他们首先在A处安置测量器，测得塔顶C的仰角∠CFE=30°，然后往塔的方向前进50米到达B处，此时测得塔顶C的仰角∠CGE=60°，已知测量器高1.5米，请你根据以上数据计算出古塔CD 的高度，（
≈1.73，
≈1.41）
查看答案和解析>>
科目：初中数学 来源： 题型：
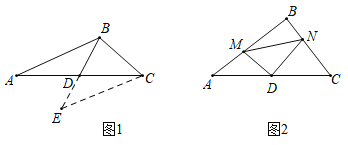
【题目】（1）阅读理解：如图1，在
中，若
，
.求
边上的中线
的取值范围.小聪同学是这样思考的：延长至
，使
，连结
.利用全等将边
转化到，在
中利用三角形三边关系即可求出中线的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________；中线的取值范围是__________.
（2）问题解决：如图2，在中，点
是的中点，点
在边上，点
在
边上，若
.求证：
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
