
����Ŀ��Ϊ��̽������ʽ![]() ����Сֵ��
����Сֵ��
С���������������ѧ˼�룮���巽���������ģ���ͼ��CΪ�߶�BD��һ���㣬�ֱ����B��D��![]() ������AC��EC����֪AB=1��DE=5��BD=8����BC=x����
������AC��EC����֪AB=1��DE=5��BD=8����BC=x����![]() ��
��![]() �����⼴ת������AC+CE����Сֵ��
�����⼴ת������AC+CE����Сֵ��
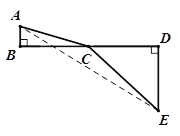
(1)����֪����A��C��E��ͬһֱ����ʱ��AC+CE��ֵ��С�����ǿ����![]() ����Сֵ���� ����ʱx= ��
����Сֵ���� ����ʱx= ��
(2)������С���������������ѧ˼������ָ������Ҫ����ѧ˼�룻
(ѡ�����˼�룬��������˼�롢���˼�롢���ν��˼��)
(3)������������ķ����ͽ��ۣ��Թ�ͼ�������ʽ![]() ����Сֵ��
����Сֵ��
���𰸡���1��10��![]() ����2�����ν��˼�룻��3��13
����2�����ν��˼�룻��3��13
��������
��1����������֮���߶���̿�֪AC+CE����Сֵ�����߶�AE�ij��ȣ�����E��EF��BD����AB���ӳ�����F�㣮��Rt��AEF�����ù��ɶ���������⣻
��2��С����������������ν��˼�룻
��3���ɣ�1���Ľ������BD=12������A��AF��BD����DE���ӳ�����F�㣬ʹAB=2��ED=3������AE��BD�ڵ�C��Ȼ�������AFDB��Rt��AFE�����þ��ε�ֱ�������ε����ʿ����AE��ֵ���Ǵ���ʽ![]() ����Сֵ��
����Сֵ��
�⣺��1������E��EF��BD����AB���ӳ�����F��

�������⣬�ı���BDEFΪ����
AF=AB+BF=5+1=6��EF=BD=8
��![]()
��AC+CE����Сֵ��10
![]()
��EF��BD
��![]()
��![]()
��ã�![]()
�ʴ�Ϊ��10��![]() ��
��
��2��С����������������ν��˼�룻
��3������A��AF��BD����DE���ӳ�����F��

�������⣬�ı���ABDFΪ����
EF=AB+DE=2+3=5��AF=DB=12
��![]()
��AC+CE����Сֵ��13��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
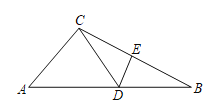
����Ŀ����ͼ����ABC�У�DΪAB��һ�㣬EΪBC��һ�㣬��AC=CD=BD=BE=2��
(1)����A=40�������CDE��
(2)��ͼ���������߶γ���Ϊ��������CE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �У�
��![]() ��
��
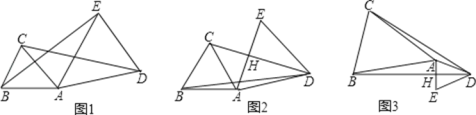
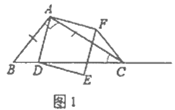
��1����ͼ1����![]() �У���
����![]() ����
����![]() ����֤��
����֤��![]() ��
��
��2����ͼ2����![]() �У���
����![]() ����
����![]() ��ֱƽ��
��ֱƽ��![]() ��
��![]() ��
��![]() ����
����![]() �ij���
�ij���
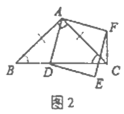
��3����ͼ3����![]() �У���
�У���![]() ��ֱƽ��
��ֱƽ��![]() ��
��![]() ����
����![]() ʱ����̽��
ʱ����̽��![]() ��
��![]() ��
��![]() ֮���������ϵ����֤����
֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
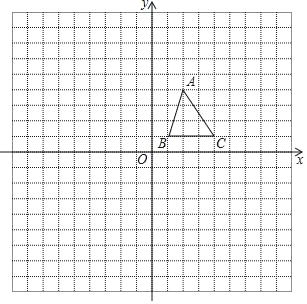
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ������ϵ������������ĵ�λ����Ϊ1����
��1���������ڻ�������ABC�Ե�OΪλ�����ĵ�λ��ͼ����A1B1C1��ʹ��A1B1C1����ABC��λ�Ʊ�Ϊ2��1����A1B1C1λ��y����ࣻ
��2���ֱ�д��A1��B1��C1����������꣺A1�� ����B1�� ����C1�� ����
��3������A1B1C1������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽�![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��1����![]() ����
����![]() �Ķ����� ��
�Ķ����� ��
��2������![]() ����
����![]() ��
��![]() ���ܳ���
���ܳ���![]() ��
��
����![]() �ij���
�ij���
����ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() ���ɵ�
���ɵ�![]() ���ܳ�ֵ��С�������ڣ������
���ܳ�ֵ��С�������ڣ������![]() ��λ�ò���
��λ�ò���![]() ���ܳ���Сֵ���������ڣ�˵�����ɣ�
���ܳ���Сֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC������B![]() 90����AB
90����AB![]() 4��BC
4��BC![]() 2����AC������ACE����ACE
2����ACΪ������ACE����ACE![]() 90����AC=CE���ӳ�BC����D��ʹCD
90����AC=CE���ӳ�BC����D��ʹCD![]() 5������DE����֤����ABC�ס�CED��
5������DE����֤����ABC�ס�CED��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���ʦΪ�˽�Ůѧ������Ͷ��������������ȡ8��Ů������ÿ��4�ζ���Ͷ���IJ��ԣ���������ͳ����ͼ��ʾ��

��1����Ů����������ƽ��������λ����
��2��Ͷ��4�Σ�����3�����ϣ���3����Ϊ���㣬ȫУ��Ů��1200�ˣ�����Ϊ�����㡱�ȼ���Ů��ԼΪ�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֪ʶ�̵�
ͨ��Сѧ��ѧϰ����֪����
�������ε������߶���ȣ��ĸ��Ƕ���ֱ������������![]() �У�
��![]() ��
��
![]() ��
��
�ڵ�������������ȵ����������Ե�������Ҳ��ȡ�����![]() �У����
�У����![]() ����ô
����ô![]() ��
��
�������
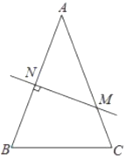
��ͼ1����![]() �У�
�У�![]() Ϊ��ǣ���
Ϊ��ǣ���![]() Ϊ����
Ϊ����![]() ��һ�㣬����
��һ�㣬����![]() ����
����![]() Ϊһ������
Ϊһ������![]() ���Ҳ���������
���Ҳ���������![]() ������������⣺
������������⣺
(1)���![]() ��
��![]()
����ͼ2������![]() ���߶�
���߶�![]() ��ʱ(���
��ʱ(���![]() ���غ�)���߶�
���غ�)���߶�![]() ��
��![]() ֮���������ϵΪ__________��λ�ù�ϵΪ__________��
֮���������ϵΪ__________��λ�ù�ϵΪ__________��
����ͼ3������![]() ���߶�
���߶�![]() ���ӳ�����ʱ�����еĽ����Ƿ���Ȼ��������˵�����ɣ�
���ӳ�����ʱ�����еĽ����Ƿ���Ȼ��������˵�����ɣ�

��չ����
��2�����![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() __________ʱ��
__________ʱ��![]() ����
����![]() ��
��![]() ���غϣ���
���غϣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
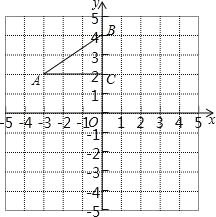
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC ����������ֱ��� A����3��2����B��0��4����C��0��2����
��1������ABC �Ե� O Ϊ��ת������ת 180�㣬������ת���Ӧ�ġ�A1B1C1��
��2��ƽ�ơ�ABC��ʹ��Ӧ�� A2 ������Ϊ��0����4����д��ƽ�ƺ��Ӧ��A2B2C2����B2��C2�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com