练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

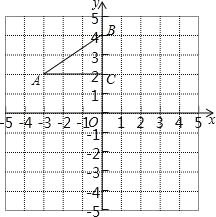
    【题目】如图，在平面直角坐标系中，Rt△ABC 的三个顶点分别是 A（﹣3，2），B（0，4），C（0，2）．

    （1）将△ABC 以点 O 为旋转中心旋转 180°，画出旋转后对应的△A1B1C1；

    （2）平移△ABC，使对应点 A2 的坐标为（0，﹣4），写出平移后对应△A2B2C2的中B2，C2点坐标．

    【答案】（1）如图所示，△A1B1C1 即为所求见解析；（2）如图所示见解析，△A2B2C2 即为所求，其中 B2 点坐标为（3，﹣2），C2 点坐标为（3，﹣4）．

    【解析】

    根据旋转作图的步骤：①定点一一旋转中心；②旋转方向；③旋转角度．再根据旋转的性质进行操作即可画出旋转之后的图形；

    接下来再根据平移作图的一般步骤，作出平移之后的图形，相信你能画出来.

    （1）如图所示，△A1B1C1 即为所求．

    （2）如图所示，△A2B2C2 即为所求，其中 B2 点坐标为（3，﹣2），C2 点坐标为（3，﹣4）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了探索代数式的最小值，

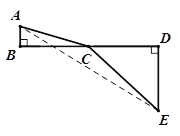
    小张巧妙的运用了数学思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作，连结AC、EC．已知AB=1，DE=5，BD=8，设BC=x．则，则问题即转化成求AC+CE的最小值．

    (1)我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得的最小值等于 ，此时x= ；

    (2)题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想；

    (选填：函数思想，分类讨论思想、类比思想、数形结合思想)

    (3)请你根据上述的方法和结论，试构图求出代数式的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

    （1）求出△ABC的面积．

    （2）在图中作出△ABC关于y轴的对称图形△A1B1C1．

    （3）写出点A1，B1，C1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

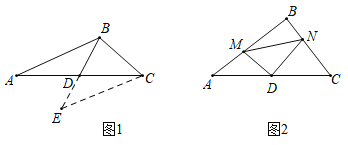
    【题目】（1）阅读理解：如图1，在中，若，.求边上的中线的取值范围.小聪同学是这样思考的：延长至，使，连结.利用全等将边转化到，在中利用三角形三边关系即可求出中线的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________；中线的取值范围是__________.

    （2）问题解决：如图2，在中，点是的中点，点在边上，点在边上，若.求证：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

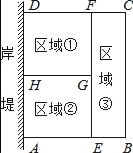
    【题目】为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80米的围网在水库中围成发如图所示①②③的三块矩形区域，而且这三块矩形区域面积相等．已知矩形区域ABCD的面积为30m2，设BC的长度为xm，所列方程为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

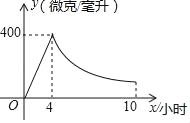
    【题目】驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾，某研究所经实验测得：成人饮用某品牌38度白酒后血液中酒精浓度y（微克/毫升）与饮酒时间x（小时）之间函数关系如图所示（当4≤x≤10时，y与x成反比例）．

    （1）根据图象分别求出血液中酒精浓度上升和下降阶段y与x之间的函数表达式．

    （2）问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3+2，善于思考的小明进行了以下探索：

    设a+b(其中a、b、m、n均为整数)，

    则有：a+b，∴a＝m2+2n2，b＝2mn，这样小明就找到了一种把类似a+b的式子化为平方式的方法．

    请你仿照小明的方法探索并解决下列问题：

    (1)当a、b、m、n均为正整数时，若a+b，用含m、n的式子分别表示a、b得：a＝　 　，b＝　 　；

    (2)利用所探索的结论，用完全平方式表示出：7+4＝　 　．

    (3)请化简：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（　　）

    A. 掷一枚均匀的骰子，骰子停止转动后，5点朝上是必然事件

    B. 明天下雪的概率为，表示明天有半天都在下雪

    C. 甲、乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别是S甲2=0.4，S乙2=0.6，则甲的射击成绩较稳定

    D. 了解一批充电宝的使用寿命，适合用普查的方式

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一不透明的布袋里，装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球2个，蓝球1个，黄球若干个，现从中任意摸出一个球是红球的概率为．

    （1）求口袋中黄球的个数；

    （2）甲同学先随机摸出一个小球（不放回），再随机摸出一个小球，请用“树状图法”或“列表法”，

    求两次摸 出都是红球的概率；

    查看答案和解析>>

    同步练习册答案