练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

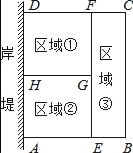
    【题目】为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80米的围网在水库中围成发如图所示①②③的三块矩形区域，而且这三块矩形区域面积相等．已知矩形区域ABCD的面积为30m2，设BC的长度为xm，所列方程为_____．

    【答案】x2﹣40x+40=0．

    【解析】

    根据三块矩形区域面积相等求出AE和BE之间关系,进而表示出AB的长度,利用总面积为30 m2即可求解.

    ∵这三块矩形区域面积相等．

    ∴S矩形AEFD=2S矩形BCFE,即AE=2EB,

    设EB=a,则AE=2a,AB=3a,

    ∴AB+HG+DC=8a,

    ∵总长为80米,设BC的长度为x米,

    ∴AB+HG+DC=80-2x=8a,整理得：a=10-x,

    ∴3x（10-x）=30,

    整理得：x2﹣40x+40=0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

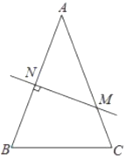
    【题目】如图，在中，，的垂直平分线交于，交于．

    （1）若，则的度数是 ；

    （2）连接，若，的周长是．

    ①求的长；

    ②在直线上是否存在点，使由，，构成的的周长值最小？若存在，标出点的位置并求的周长最小值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知:r如图，在梯形ABCD中，AD∥BC，∠BCD=90°.对角线AC、BD相交于点E。且AC⊥BD。（1）求证：CD=BC·AD；（2）点F是边BC上一点，连接AF，与BD相交于点G，如果∠BAF=∠DBF，求证：。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品的进价为每件50元，售价为每件60元，每个月可卖出200件；如果每件商品的售价每上涨1元．则每个月少卖10件．设每件商品的售价上涨x元（x为正整数），每个月的销售利润为y元．

    （1）求y与x的函数关系式；

    （2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

    （3）若每个月的利润不低于2160元，售价应在什么范围？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80米的围网在水库中围成发如图所示①②③的三块矩形区域，而且这三块矩形区域面积相等．已知矩形区域ABCD的面积为30m2，设BC的长度为xm，所列方程为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

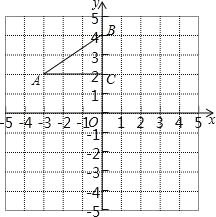
    【题目】如图，在平面直角坐标系中，Rt△ABC 的三个顶点分别是 A（﹣3，2），B（0，4），C（0，2）．

    （1）将△ABC 以点 O 为旋转中心旋转 180°，画出旋转后对应的△A1B1C1；

    （2）平移△ABC，使对应点 A2 的坐标为（0，﹣4），写出平移后对应△A2B2C2的中B2，C2点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在⊙O中，弦AD，BC相交于点E，连接OE，已知AD＝BC，AD⊥CB．

    （1）求证：AB＝CD；

    （2）如果⊙O的直径为10，DE＝1，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

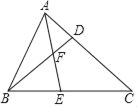
    【题目】如图，已知点D、E分别在△ABC的边AC、BC上，线段BD与AE交于点F，且CDCA=CECB．

    （1）求证：∠CAE=∠CBD；

    （2）若，求证：ABAD=AFAE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A（―3，6）、B（―9，一3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（ ）

    A．（―1，2）

    B．（―9，18）

    C．（―9，18）或（9，―18）

    D．（―1，2）或（1，―2）

    查看答案和解析>>

    同步练习册答案