
【题目】已知:r如图,在梯形ABCD中,AD∥BC,∠BCD=90°.对角线AC、BD相交于点E。且AC⊥BD。(1)求证:CD=BC·AD;(2)点F是边BC上一点,连接AF,与BD相交于点G,如果∠BAF=∠DBF,求证:![]() 。
。

【答案】见解答过程.
【解析】
试题(1)首先根据已知得出∠ACD=∠CBD,以及∠ADC=∠BCD=90°,进而求出△ACD∽△DBC,即可得出答案;
(2)首先证明△ABG∽△DBA,进而得出AG:AD=AB:BD,再利用△ABG∽△DBA,得出BG:AB="AB:BD" ,则AB2=BGBD,进而得出答案.
试题解析:证明:(1)∵AD∥BC,∠BCD=90°,
∴∠ADC=∠BCD=90°,
又∵AC⊥BD,∴∠ACD+∠ACB=∠CBD+∠ACB=90°,
∴∠ACD=∠CBD,
∴△ACD∽△DBC,
∴AD CD ="CD" BC ,
即CD2=BC×AD;
(2)∵AD∥BC,∴∠ADB=∠DBF,
∵∠BAF=∠DBF,∴∠ADB=∠BAF,
∵∠ABG=∠DBA,∴△ABG∽△DBA,
∴S△ABG:S△DBA =(![]() )2=AG2:AD2,
)2=AG2:AD2,
而S△ABG:S△DBA="BG:BD" ,∴AG2:AD2 ="BG:BD" .


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=![]() BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
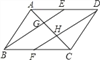
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小杰想用6个除颜色外均相同的球设计一个游戏,下面是他设计的4个游戏方案.不成功的是( )
A. 摸到黄球的概率为![]() ,红球的概率为
,红球的概率为![]()
B. 摸到黄、红、白球的概率都为![]()
C. 摸到黄球的概率为![]() ,红球的概率为
,红球的概率为![]() ,白球的概率为
,白球的概率为![]()
D. 摸到黄球的概率为![]() ,摸到红球、白球的概率都是
,摸到红球、白球的概率都是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据: ![]() ≈1.414,、
≈1.414,、![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积.
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1.
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进A、B两种商品,若购进A种商品5件和B种商品4件需300元;若购进A种商品6件和B种商品8件需440元;
(1)求A、B两种商品每件的进价分别为多少元?
(2)商店准备用不超过1625元购进50件这两种商品,求购进A种商品最多是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
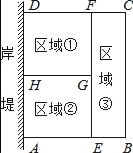
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成发如图所示①②③的三块矩形区域,而且这三块矩形区域面积相等.已知矩形区域ABCD的面积为30m2,设BC的长度为xm,所列方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
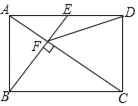
A. AF=![]() CF B. ∠DCF=∠DFC
CF B. ∠DCF=∠DFC
C. 图中与△AEF相似的三角形共有5个 D. tan∠CAD=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com