
【题目】如图,在平面直角坐标系中,矩形![]() 的直角边
的直角边![]() 、
、![]() 分别在
分别在![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴上,过点
轴的正半轴上,过点![]() 的直线
的直线![]() 交矩形的
交矩形的![]() 边于点
边于点![]() ,
, ![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)若把![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 轴上的点
轴上的点![]() 处,
处,
①求![]() 与
与![]() 的函数关系式(不需写出
的函数关系式(不需写出![]() 的范围);
的范围);
②当![]() 时,在坐标轴上是否存在点
时,在坐标轴上是否存在点![]() ,使得
,使得![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 、
、![]() 、
、![]() 、
、![]()
【解析】试题分析:(1)由![]() ,可知点G纵坐标为b,把y=b代入
,可知点G纵坐标为b,把y=b代入![]() 中,解得
中,解得![]() ,可得点
,可得点![]() 的坐标.(2)① 由矩形性质可知
的坐标.(2)① 由矩形性质可知![]() 在
在![]() 中,令x=0,得y=b,得
中,令x=0,得y=b,得![]() ,由翻折
,由翻折![]() ,由一线三等角得
,由一线三等角得![]() ∽
∽![]() ,则对应边成比例,得
,则对应边成比例,得![]() ,在
,在![]() 中,由勾股定理可得
中,由勾股定理可得![]() 与
与![]() 的函数关系式;②
的函数关系式;②![]() ,可得
,可得![]() ,
, ![]() ,分情况讨论:
,分情况讨论: ![]() ,
, ![]() ,所以点
,所以点![]() 为符合题意的点;
为符合题意的点; ![]() 可得
可得![]() 轴,符合题意;在直线
轴,符合题意;在直线![]() 中,直线与
中,直线与![]() 轴的交点
轴的交点![]() ,也是符合题意的点;
,也是符合题意的点; ![]() 可知
可知![]() 是符合题意的点.
是符合题意的点.
试题解析:(1)当![]() 时,
时, ![]() ,解得:
,解得: ![]()
∴点![]() 的坐标为
的坐标为![]()
(2)①∵四边形![]() 是矩形,∴
是矩形,∴![]()
在![]() 中,当
中,当![]() 时,
时, ![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 关于
关于![]() 对称,
对称,
∴![]() ,
, ![]() ,
,
∴![]()
又![]() ,
,
∴![]()
又![]() ,∴
,∴![]() ∽
∽![]() ,
,
∴![]() ,
, ![]() ,解得:
,解得: ![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得: ![]() ,
, ![]() ,解得:
,解得: ![]() .
.
②![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
i) ![]() ,
, ![]() ,
,
∴点![]() 为符合题意的点,此时点
为符合题意的点,此时点![]() .
.
ii) ![]()

∴![]()
∵![]() ,∴
,∴![]() 轴,
轴, ![]() .
.
iii)在直线![]() 中,令
中,令![]() ,则
,则![]() ,
,
∴直线![]() 与
与![]() 轴的交点
轴的交点![]() ,
,
在![]() 中,
中, ![]() ,
,
∴点![]() 是符合题意的点.
是符合题意的点.
iv)点![]() 是关于
是关于![]() 的
的![]() 点为点
点为点![]() ,此时
,此时![]() ,
,
∴点![]() 是符合题意的点.
是符合题意的点.
综上,符合题意的点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 、
、![]() .
.


科目:初中数学 来源: 题型:
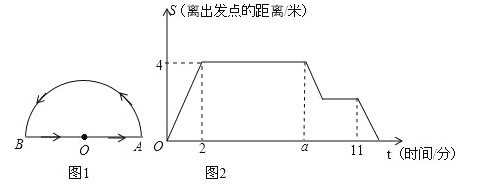
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)请直接写出:花坛的半径是 米,a= .
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回O的时间.(注:圆周率π的值取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有点A(0,4)、B(9,4)、C(12,0).已知点P从点A出发沿着AB路线向点B运动,点Q从点C出发沿CO路线向点O运动,运动速度都是每秒2个单位长度,运动时间为t秒.
(1)当t=4.5秒时,判断四边形AQCB的形状,并说明理由.
(2)当四边形AOQB是矩形时,求t的值.
(3)是否存在某一时刻,使四边形PQCB是菱形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
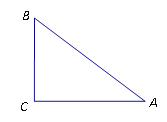
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
(1) ![]() _______________;
_______________;
(2)若经过点![]() 且与边
且与边![]() 相切的动圆与边
相切的动圆与边![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() ,则线段
,则线段![]() 长度的取值范围是_________________.
长度的取值范围是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解一批电视机的寿命,从中抽取100台电视机进行试验,这个问题中的样本是( )
A.这批电视机的寿命B.抽取的100台电视机
C.100D.抽取的100台电视机的寿命
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两个样本,甲的样本方差是0.065,乙的样本方差是0.056,那么样本甲与样本乙的波动大小应是 ( )
A. 甲的波动比乙的大 B. 甲的波动比乙的小
C. 甲与乙的波动相同 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有五名销售员,2007年平均每人每月的销售额分别是6,8,11,9,8(万元),现公司需增加一名销售员,三人应聘试用三个月,平均每人每月的销售额分别为:甲是上述数据的平均数,乙是中位数,丙是众数,最后录用三人中平均月销售额最高的人是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com