
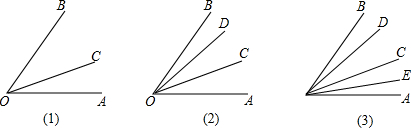
分析 根据题意,从基本图形出发,看每一次所得锐角个数比上一次增加多少个锐角,寻找一般规律即可得出答案.
解答 解:∵在锐角∠AOB内部,画1条射线,可得1+2=3个锐角;
在锐角∠AOB内部,画2条射线,可得1+2+3=6个锐角;
在锐角∠AOB内部,画3条射线,可得1+2+3+4=10个锐角;
…
∴从一个角的内部引出(n-2)条射线所得到的锐角的个数是:
1+2+3+…+(n-1)=$\frac{1}{2}$n(n-1).
故答案为:$\frac{1}{2}$n(n-1).
点评 本题主要考查了角的概念以及数字变化规律,注意得出从一个角的内部引出n条射线所得到的锐角的个数是 $\frac{1}{2}$×(n+1)×(n+2)是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时:
如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com