
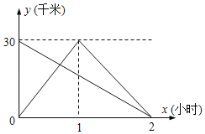
【题目】在一条笔直的公路上有AB两地,小明骑自行车从A地去B地,小刚骑电动车从B地去A地然后立即原路返回到B地,如图是两人离B地的距离y(千米)和行驶时间x(小时)之间的函数图象.请根据图象回答下列问题:
(1)AB两地的距离是_____,小明行驶的速度是_____.
(2)若两人间的距离不超过3千米时,能够用无线对讲机保持联系,那么小刚从A地原路返回到B地途中,两人能够用无线对讲机保持联系的x的取值范围是______.
【答案】(1)30km;15km/h;(2)![]() .
.
【解析】
(1)根据图象即可解决问题;
(2)根据图象和待定系数法分别求出小刚从A地原路返回到B地时对应的一次函数![]() 和小明从A地到B地对应的一次函数
和小明从A地到B地对应的一次函数![]() ,再求出当
,再求出当![]() 时x的值即可求出答案.
时x的值即可求出答案.
解:(1)x=0时,小明距离B地30km,所以,A、B两地的距离为30km;
由图可知,小明行驶的速度:30÷2=15(km/h),小刚行驶的速度:30÷1=30(km/h),
(2)设小刚从A地原路返回到B地时对应的一次函数解析式为![]() ,小明从A地到B地对应的一次函数解析式为
,小明从A地到B地对应的一次函数解析式为![]() ,则
,则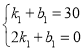 ,
, ,
,
解得: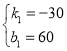 ,
, ,
,
∴![]() ,
,![]() ,
,
根据题意,当![]() 时,
时,![]() ,解得
,解得![]() ,
,
所以,当![]() 时,小刚从A地原路返回到B地途中,两人能够用无线对讲机保持联系.
时,小刚从A地原路返回到B地途中,两人能够用无线对讲机保持联系.
故答案为:(1)30km;15km/h;(2)![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.
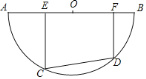
(1)求证:EO=OF;
(2)联结OC,如果△ECO中有一个内角等于45°,求线段EF的长;
(3)当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE面积为S,周长为l,问:S与l是否分别随着x的变化而变化?试用所学的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,DB⊥BC,DB平分∠ADC,点E为边CD的中点,AB⊥BE.
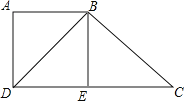
(1)求证:BD2=ADDC;
(2)连结AE,当BD=BC时,求证:ABCE为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AC、BD相交于点O,AB⊥AC,AD=CD,AB=3,BC=5.求:
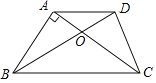
(1)tan∠ACD的值;
(2)梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的倾斜角∠BAH=30°,AB=20米,AB=30米.
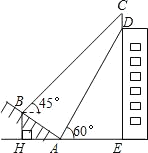
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
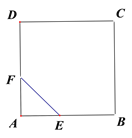
【题目】如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,联接EF,将△AEF绕点A逆时针旋转45°,使E落在E![]() ,F落在F
,F落在F![]() ,联接BE
,联接BE![]() 并延长交DF
并延长交DF![]() 于点G,如果AB=
于点G,如果AB=![]() ,AE=1,则DG=______.
,AE=1,则DG=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某林业部门统计某种树苗在本地区一定条件下的移植成活率,结果如表:
移植的棵数 | 300 | 700 | 1000 | 5000 | 15000 |
成活的棵数 | 280 | 622 | 912 | 4475 | 13545 |
成活的频率 | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
根据表中的数据,估计这种树苗移植成活的概率为_____(精确到0.1);如果该地区计划成活4.5万棵幼树,那么需要移植这种幼树大约_____万棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假期小颖决定到游泳馆游泳,游泳馆门票有两种:![]() 种是每天购票进馆,没有优惠;
种是每天购票进馆,没有优惠;![]() 种是每月先购买贵宾卡,持贵宾卡购票每张可减少8元.设小颖游泳
种是每月先购买贵宾卡,持贵宾卡购票每张可减少8元.设小颖游泳![]() 次,
次,![]() (元)是按
(元)是按![]() 种购票方案的费用,
种购票方案的费用,![]() (元)是按
(元)是按![]() 种购票方案的费用根据图中信息解答问题:
种购票方案的费用根据图中信息解答问题:
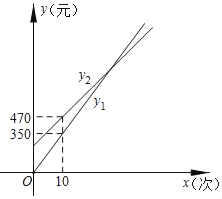
(1)按![]() 种方案购票,每张门票价格为 元;
种方案购票,每张门票价格为 元;
(2)按![]() 种方案购票,求
种方案购票,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)如果小颖假期30天,每天都到游泳馆游泳一次,通过计算她选择哪种购票方案比较合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com