
【题目】如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的倾斜角∠BAH=30°,AB=20米,AB=30米.
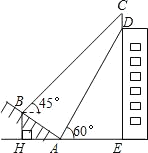
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
【答案】(1) BH为10米;(2) 宣传牌CD高约(40﹣20![]() )米
)米
【解析】
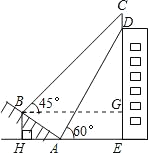
(1)过B作DE的垂线,设垂足为G.分别在Rt△ABH中,通过解直角三角形求出BH、AH;
(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE-DE即可求出宣传牌的高度.
(1)过B作BH⊥AE于H,
Rt△ABH中,∠BAH=30°,
∴BH=![]() AB=
AB=![]() ×20=10(米),
×20=10(米),
即点B距水平面AE的高度BH为10米;
(2)过B作BG⊥DE于G,
∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.
∵由(1)得:BH=10,AH=10![]() ,
,
∴BG=AH+AE=(10![]() +30)米,
+30)米,
Rt△BGC中,∠CBG=45°,
∴CG=BG=(10![]() +30)米,
+30)米,
∴CE=CG+GE=CG+BH=10![]() +30+10=10
+30+10=10![]() +40(米),
+40(米),
在Rt△AED中,
![]() =tan∠DAE=tan60°=
=tan∠DAE=tan60°=![]() ,
,
DE=![]() AE=30
AE=30![]()
∴CD=CE﹣DE=10![]() +40﹣30
+40﹣30![]() =40﹣20
=40﹣20![]() .
.
答:宣传牌CD高约(40﹣20![]() )米.
)米.


科目:初中数学 来源: 题型:
【题目】2017年歌舞剧《白毛女》将在广州歌舞剧院公演,对团体购买门票实行优惠,决定在原定票价基础上每张降价![]() 元,这样按原定票价需花费
元,这样按原定票价需花费![]() 元购买的门票现在只需花费了
元购买的门票现在只需花费了![]() 元就可以买到了.
元就可以买到了.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续两次降价后降为![]() 元,求平均每次降价的百分率.
元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边AB是⊙O的直径,点C在⊙O上,已知AC=6cm,BC=8cm,点P、Q分别在边AB、BC上,且点P不与点A、B重合,BQ=kAP(k>0),联接PC、PQ.
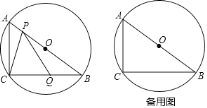
(1)求⊙O的半径长;
(2)当k=2时,设AP=x,△CPQ的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△CPQ与△ABC相似,且∠ACB=∠CPQ,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子_____.
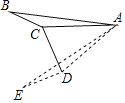
查看答案和解析>>
科目:初中数学 来源: 题型:
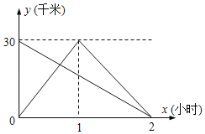
【题目】在一条笔直的公路上有AB两地,小明骑自行车从A地去B地,小刚骑电动车从B地去A地然后立即原路返回到B地,如图是两人离B地的距离y(千米)和行驶时间x(小时)之间的函数图象.请根据图象回答下列问题:
(1)AB两地的距离是_____,小明行驶的速度是_____.
(2)若两人间的距离不超过3千米时,能够用无线对讲机保持联系,那么小刚从A地原路返回到B地途中,两人能够用无线对讲机保持联系的x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
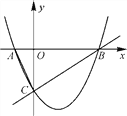
【题目】如图,已知直线![]() 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线![]()
与x轴交于A、B两点(A在B的左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)点M是上述抛物线上一点,如果△ABM和△ABC相似,求点M的坐标;
(3)连接AC,求顶点D、E、F、G在△ABC各边上的矩形DEFC面积最大时,写出该矩形在AB边上的顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
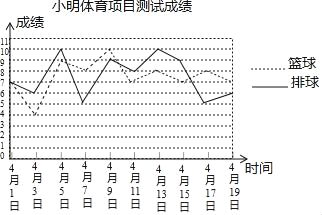
【题目】在体育中考项目中考生可在篮球、排球中选考一项.小明为了选择一项参加体育中考,将自己的10次测验成绩进行比较并制作了折线统计图,依据图中信息小明选择哪一项参加体育中考更合适,并说明理由,______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为射线
为射线![]() 上一点(与点
上一点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 于点
于点![]() ,且
,且![]() (点
(点![]() 与点
与点![]() 在射线
在射线![]() 同侧),连接
同侧),连接![]() ,
,![]() .
.
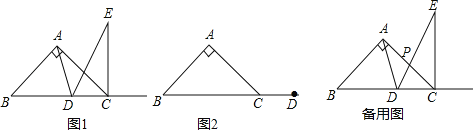
(1)如图1,当点![]() 在线段
在线段![]() 上时,请直接写出
上时,请直接写出![]() 的度数.
的度数.
(2)当点![]() 在线段
在线段![]() 的延长线上时,依题意在图2中补全图形并判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.
的延长线上时,依题意在图2中补全图形并判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.
(3)在(1)的条件下,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,直接写出
,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
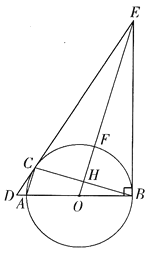
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC。
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若CF=6,sin∠FCB=![]() ,求AC的长。
,求AC的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com