
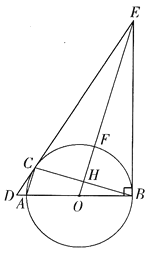
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC。
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若CF=6,sin∠FCB=![]() ,求AC的长。
,求AC的长。
【答案】(1)证明见解析;
(2)AC的长为![]()
【解析】试题分析:(1)只要证明EB是⊙O的切线,利用切线长定理可知EC=EB,即可解决问题.
(2)连接CF、CO、AC.在Rt△CFH中,由CF=6,sin∠FCH=![]() ,推出FH=CFsin∠FCH=
,推出FH=CFsin∠FCH=![]() ,CH=
,CH=![]() ,设OC=OF=x,在Rt△COH中,由OC2=CH2+OH2,可得x2=(
,设OC=OF=x,在Rt△COH中,由OC2=CH2+OH2,可得x2=(![]() )2+(x-
)2+(x-![]() )2,解得x=5,推出OH=
)2,解得x=5,推出OH=![]() ,再利用三角形中位线定理证明AC=2OH即可解决问题.
,再利用三角形中位线定理证明AC=2OH即可解决问题.
试题解析:(1)证明:∵BE⊥OB,
∴BE是⊙O的切线,∵EC是⊙O的切线,
∴EC=EB,
∴∠ECB=∠EBC.
(2)连接CF、CO、AC.
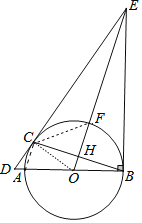
∵EB=EC,OC=OB,
∴EO⊥BC,
∴∠CHF=∠CHO=90°,
在Rt△CFH中,∵CF=6,sin∠FCH=![]() ,
,
∴FH=CFsin∠FCH=![]() ,CH=
,CH=![]() ,
,
设OC=OF=x,
在Rt△COH中,∵OC2=CH2+OH2,
∴x2=(![]() )2+(x-
)2+(x-![]() )2,
)2,
∴x=5,
∴OH=![]() ,
,
∵OH⊥BC,
∴CH=HB,∵OA=OB,
∴AC=2OH=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
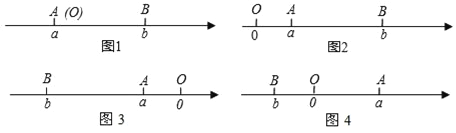
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
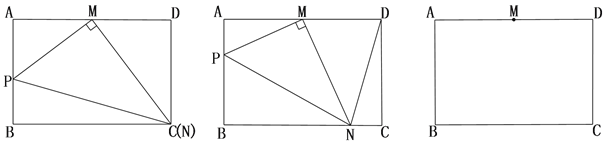
【题目】在矩形ABCD中,AB=4,AD=6,M是AD边的中点,P是射线AB上的一个动点(不与A、B重合),MN⊥PM交射线BC于N点.
(1)如图1,当点N与点C重合时,求:AP的长;
(2)如图2,在点N的运动过程中,求证: ![]() 为定值;
为定值;
(3)在射线AB上,是否存在点P,使得![]() ∽
∽![]() ,若存在,求此时AP的长;若不存在,请说明理由.
,若存在,求此时AP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件:①.在足球比赛中,中国男足战胜德国男足;②.有交通信号灯的路口遇到红灯;③.连续两次抛掷一枚普通的正方体骰子得到的点数之和为13;④.任取一数为x,使它满足x3=x2.其中随机事件有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点.如果两个正方形的边长都等于2,那么正方形A′B′C′OA绕O点无论怎样转动,两个正方形重叠的部分的面积是 . 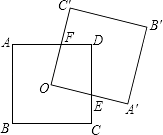
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com