
【题目】2017年歌舞剧《白毛女》将在广州歌舞剧院公演,对团体购买门票实行优惠,决定在原定票价基础上每张降价![]() 元,这样按原定票价需花费
元,这样按原定票价需花费![]() 元购买的门票现在只需花费了
元购买的门票现在只需花费了![]() 元就可以买到了.
元就可以买到了.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续两次降价后降为![]() 元,求平均每次降价的百分率.
元,求平均每次降价的百分率.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
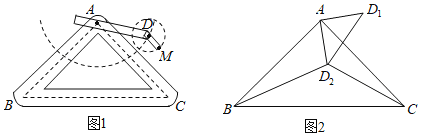
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂
的等腰直角三角形,摆动臂![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
(1)在旋转过程中,当![]() 为同一直角三角形的顶点时,
为同一直角三角形的顶点时,![]() 的长为______________.
的长为______________.
(2)若摆动臂![]() 顺时针旋转90°,点
顺时针旋转90°,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,
,![]() 的长为______________.
的长为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽度为20 m,长为32 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540 m2 , 求道路的宽.如果设小路宽为x m,根据题意,所列方程正确的是( )
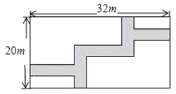
A.(20+x)(32+x)=540
B.(20﹣x)(32﹣x)=100
C.(20﹣x)(32﹣x)=540
D.(20-2x)(32﹣2x)=540
查看答案和解析>>
科目:初中数学 来源: 题型:
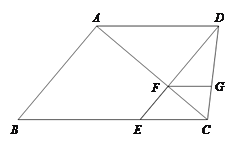
【题目】已知:如图,梯形ABCD中,AD∥BC,DE∥AB,![]() 与对角线
与对角线![]() 交于点
交于点![]() ,
,![]() ∥
∥![]() ,且FG=EF.
,且FG=EF.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)联结AE,又知AC⊥ED,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D,E分别为△ABC的边AB,BC上两点,点A,C,E在⊙D上,点B,D在⊙E上.F为![]() 上一点,连接FE并延长交AC的延长线于点N,交AB于点M.
上一点,连接FE并延长交AC的延长线于点N,交AB于点M.
(1)若∠EBD为α,请将∠CAD用含α的代数式表示;
(2)若EM=MB,请说明当∠CAD为多少度时,直线EF为⊙D的切线;
(3)在(2)的条件下,若AD=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴,y轴分别交于点A(2,0),点B(0,2![]() ),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以
),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以![]() 个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F
个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F
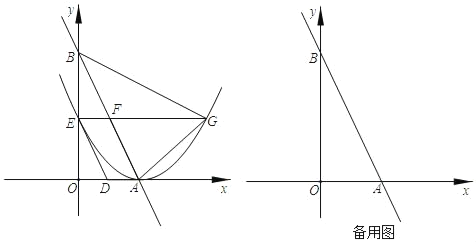
(1)求∠OAB度数;
(2)当t为何值时,四边形ADEF为菱形,请求出此时二次函数解析式;
(3)是否存在实数t,使△AGF为直角三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,与y轴相交于点C,顶点为P.
,与y轴相交于点C,顶点为P.
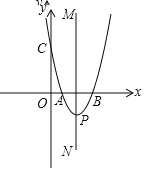
(1)求这条抛物线的表达式和顶点P的坐标;
(2)点E在抛物线的对称轴上,且![]() ,求点E的坐标;
,求点E的坐标;
(3)在(2)的条件下,记抛物线的对称轴为直线MN,点Q在直线MN右侧的抛物线上,![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的倾斜角∠BAH=30°,AB=20米,AB=30米.
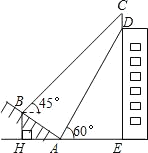
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com