
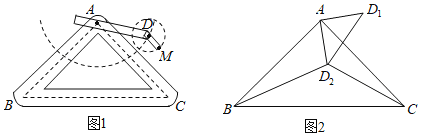
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂
的等腰直角三角形,摆动臂![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
(1)在旋转过程中,当![]() 为同一直角三角形的顶点时,
为同一直角三角形的顶点时,![]() 的长为______________.
的长为______________.
(2)若摆动臂![]() 顺时针旋转90°,点
顺时针旋转90°,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,
,![]() 的长为______________.
的长为______________.
【答案】20![]() 或10
或10![]() ; 30
; 30![]() .
.
【解析】
(1)显然∠MAD不能为直角,当∠AMD为直角和当∠ADM为直角时,根据勾股定理计算即可;
(2)连接CD,首先利用勾股定理求出CD1,再利用全等三角形的性质证明BD2=CD1即可.
解:(1)显然∠MAD不能为直角.
当∠AMD=90°时,AM2=AD2﹣DM2=302﹣102=800,∴AM=20![]() 或﹣20
或﹣20![]() (舍去);
(舍去);
当∠ADM=90°时,AM2=AD2+DM2=302+102=1000,∴AM=10![]() 或﹣10
或﹣10![]() (舍去).
(舍去).
综上所述,满足条件的AM的值为20![]() 或10
或10![]() .
.
(2)如图2中,连接CD.
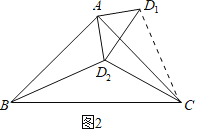
由题意:∠D1AD2=90°,AD1=AD2=30,
∴∠AD2D1=45°,D1D2=30![]() ,
,
∵∠AD2C=135°,∴∠CD2D1=90°,
∴CD1=![]() =30
=30![]() ,
,
∵∠BAC=∠D1AD2=90°,
∴∠BAD2=∠CAD1,
∵AB=AC,AD2=AD1,
∴△BAD2≌△CAD1(SAS),
∴BD2=CD1=30![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣1和抛物线L:y=ax2+bx+c(a≠0),抛物线L的顶点为原点,且经过点A(2![]() ,
,![]() ),直线y=kx+1与y轴交于点F,与抛物线L交于点B(x1,y1),C(x2,y2),且x1<x2.
),直线y=kx+1与y轴交于点F,与抛物线L交于点B(x1,y1),C(x2,y2),且x1<x2.
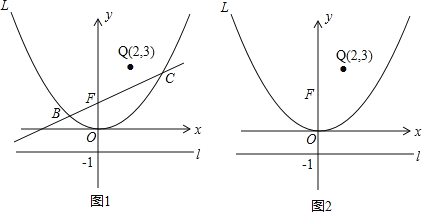
(1)求抛物线L的解析式;
(2)点P是抛物线L上一动点.
①以点P为圆心,PF为半径作⊙P,试判断⊙P与直线l的位置关系,并说明理由;
②若点Q(2,3),当|PQ﹣PF|的值最小时,求点P的坐标;
(3)求证:无论k为何值,直线l总是与以BC为直径的圆相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
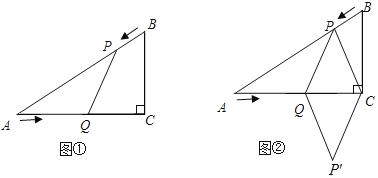
【题目】已知:如图①,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,PQ∥BC;
(2)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为“单人组”和“双人组”.小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=![]() ,弦BM平分∠ABC交AC于点D,连接MA,MC.
,弦BM平分∠ABC交AC于点D,连接MA,MC.
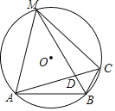
(1)试判断![]() 的形状;
的形状;
(2)求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年歌舞剧《白毛女》将在广州歌舞剧院公演,对团体购买门票实行优惠,决定在原定票价基础上每张降价![]() 元,这样按原定票价需花费
元,这样按原定票价需花费![]() 元购买的门票现在只需花费了
元购买的门票现在只需花费了![]() 元就可以买到了.
元就可以买到了.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续两次降价后降为![]() 元,求平均每次降价的百分率.
元,求平均每次降价的百分率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com