
【题目】图象经过三点![]() ,
,![]() 和
和![]() (
(![]() )的函数只可能是( )
)的函数只可能是( )
A.正比例函数B.一次函数C.反比例函数D.二次函数
【答案】D
【解析】
依次分析正比例函数,一次函数,可得出这三点不在同一直线上,故不可能是正比例函数和一次函数,若为反比例函数,分析可得出互相矛盾的结论,故只能是二次函数.
解:设A![]() ,B
,B![]() ,C
,C![]() (
(![]() ),函数的图象过点A和B,
),函数的图象过点A和B,
(1)若为正比例函数,设解析式为y=kx, 函数的图象过点A![]() 和B,,易得k=3,
和B,,易得k=3,
∴y=3x,
把B![]() 代入,得
代入,得![]() ,
,
解得![]() ,则
,则![]() ,即C(3,-4),
,即C(3,-4),
易知C(3,-4)不在直线y=3x上,故这个函数不可能是正比例函数;
(2)若为一次函数,且过点B![]() 和点C
和点C![]() (
(![]() ),设y=kx+b,则有:
),设y=kx+b,则有: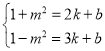 ,
,
解得:![]() (
(![]() )
)
则当x=1时,![]()
所以A![]() 不在直线
不在直线![]() 上,
上,
故这个函数不可能是一次函数;
(3)若为反比例函数,设![]() ,将A
,将A![]() 代入可得k=4,即
代入可得k=4,即![]()
将B![]() 代入
代入![]() ,可得
,可得![]() ,
,
将C![]() 代入
代入![]() ,可得
,可得![]() ,与前面矛盾且无解,
,与前面矛盾且无解,
故这个函数不可能是反比例函数;
(4)综上可知,点A,B,C不在同一直线上,因此过这三点可得一抛物线,即这个函数只可能是二次函数.
故选:D


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
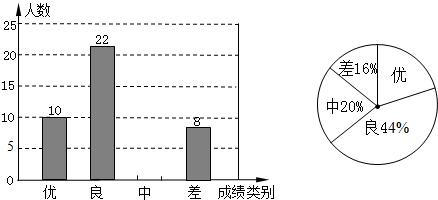
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)求本中学成绩类别为“中”的人数;
(2)求出扇形图中,“优”所占的百分比,并将条形统计图补充完整;
(3)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )

A. 15°和(2,1+![]() )
)
B. 75°和(2,![]() ﹣1)
﹣1)
C. 15°和(2,1+![]() )或75°和(2,
)或75°和(2,![]() ﹣1)
﹣1)
D. 15°和(2,1+![]() )或75°和(2,1﹣
)或75°和(2,1﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
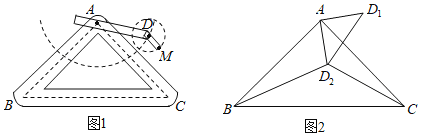
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂
的等腰直角三角形,摆动臂![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
(1)在旋转过程中,当![]() 为同一直角三角形的顶点时,
为同一直角三角形的顶点时,![]() 的长为______________.
的长为______________.
(2)若摆动臂![]() 顺时针旋转90°,点
顺时针旋转90°,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,
,![]() 的长为______________.
的长为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级上学期,我们探究了“设计制作长方体形状的包装纸盒”,今天我们继续运用所学知识,解决“设计制作长方体形状的包装纸盒”中常见的问题.如图1是一块边长为60cm 的正方形薄铁片,现在用它来制作成如图2的一个长方体盒子.
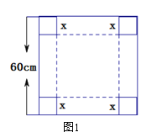
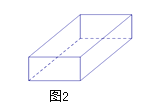

(1)如果要做成一个没有盖的长方体盒子,可先在薄铁片的四个角上截去四个相同的小正方形,边长为xcm, 然后把四边折合起来.
①求做成的盒子底面积ycm2与截去小正方形边长xcm之间的函数关系式;
②当做成的盒子的底面积为900cm2时,试求该盒子的容积.
(2)如果要做成一个有盖的长方体盒子,其制作方案要求同时符合下列两个条件:
①必须在薄铁片的四个角上各截去一个四边形(其余部分不能裁截);
②折合后薄铁片既无空隙、又不重叠地围成各盒面,请你画出符合上述制作方案的一种草案(不必说明画法与根据),并求当底面积为800cm2时,该盒子的高.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,
上一点,![]() ,过点
,过点![]() 三点的
三点的![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]()
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)若![]() ,请用题意可以推出的结论说明命题:“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题
,请用题意可以推出的结论说明命题:“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题

查看答案和解析>>
科目:初中数学 来源: 题型:
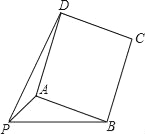
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
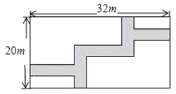
【题目】如图,在宽度为20 m,长为32 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540 m2 , 求道路的宽.如果设小路宽为x m,根据题意,所列方程正确的是( )
A.(20+x)(32+x)=540
B.(20﹣x)(32﹣x)=100
C.(20﹣x)(32﹣x)=540
D.(20-2x)(32﹣2x)=540
查看答案和解析>>
科目:初中数学 来源: 题型:
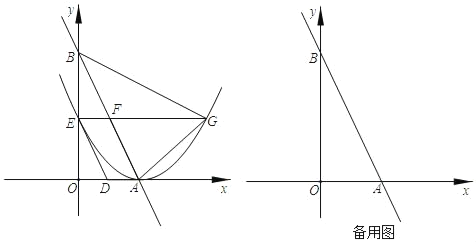
【题目】如图,直线AB与x轴,y轴分别交于点A(2,0),点B(0,2![]() ),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以
),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以![]() 个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F
个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F
(1)求∠OAB度数;
(2)当t为何值时,四边形ADEF为菱形,请求出此时二次函数解析式;
(3)是否存在实数t,使△AGF为直角三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com